Bài 3 trang 99 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Bài 3 trang 99 SGK Toán 11 tập 2 - Cánh Diều
Bài 3 trang 99 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc luyện tập về đạo hàm của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tính đạo hàm của các hàm số lượng giác và hàm hợp.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Chứng minh các định lí sau:
Đề bài
Chứng minh các định lí sau:
a) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó;
b) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt còn lại.
Phương pháp giải - Xem chi tiết
Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
Lời giải chi tiết
a)
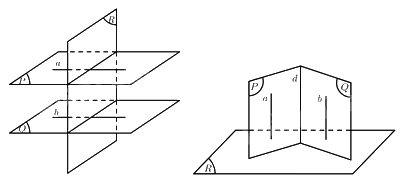
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Ta cần chứng minh \(\left( P \right)\parallel \left( Q \right)\) hoặc \(d \bot \left( R \right)\) với \(d = \left( P \right) \cap \left( Q \right)\).
Vì \(\left( P \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(a \subset \left( P \right)\) sao cho \(a \bot \left( R \right)\), \(\left( Q \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(b \subset \left( Q \right)\) sao cho \(b \bot \left( R \right)\)
\( \Rightarrow a\parallel b\)
Vậy \(\left( P \right)\parallel \left( Q \right)\) hoặc nếu \(\left( P \right),\left( Q \right)\) cắt nhau theo giao tuyến \(d\) thì \(d\parallel a \Rightarrow d \bot \left( R \right)\).
b)
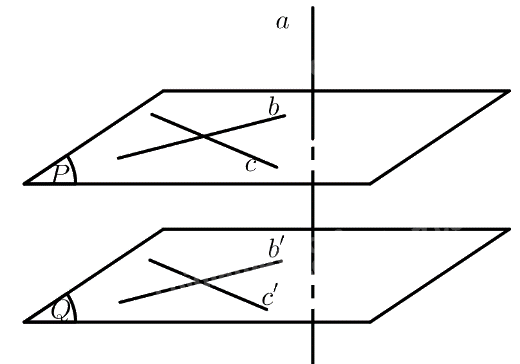
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) song song với nhau và đường thẳng \(a\) vuông góc với \(\left( P \right)\). Ta cần chứng minh \(a \bot \left( Q \right)\).
Trên \(\left( P \right)\) lấy hai đường thẳng \(b,c\) cắt nhau, trên \(\left( Q \right)\) lấy hai đường thẳng \(b',c'\) sao cho \(b'\parallel b,c'\parallel c\).
Vì \(b,c\) cắt nhau nên \(b',c'\) cắt nhau.
\(\begin{array}{l}\left. \begin{array}{l}a \bot \left( P \right) \Rightarrow a \bot b,a \bot c\\b\parallel b',c\parallel c'\end{array} \right\} \Rightarrow a \bot b',a \bot c'\\ \Rightarrow a \bot \left( Q \right)\end{array}\)
Bài 3 trang 99 SGK Toán 11 tập 2 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 3 trang 99 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học về đạo hàm. Bài tập này giúp học sinh củng cố kiến thức về cách tính đạo hàm của các hàm số lượng giác và hàm hợp, đồng thời rèn luyện kỹ năng giải toán.
Nội dung bài tập
Bài 3 yêu cầu tính đạo hàm của các hàm số sau:
- a) y = sin(x^2 + 1)
- b) y = cos(2x - π/3)
- c) y = tan(x^3)
- d) y = cot(√(x + 1))
Phương pháp giải
Để giải bài tập này, chúng ta cần sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x). Ngoài ra, cần nhớ các công thức đạo hàm cơ bản của các hàm số lượng giác:
- (sin x)' = cos x
- (cos x)' = -sin x
- (tan x)' = 1/cos^2 x
- (cot x)' = -1/sin^2 x
Giải chi tiết
a) y = sin(x^2 + 1)
Đặt u = x^2 + 1, v = u. Khi đó, y = sin(u). Ta có:
- u' = 2x
- v' = cos(u)
Vậy, y' = cos(x^2 + 1) * 2x = 2x * cos(x^2 + 1)
b) y = cos(2x - π/3)
Đặt u = 2x - π/3, v = u. Khi đó, y = cos(u). Ta có:
- u' = 2
- v' = -sin(u)
Vậy, y' = -sin(2x - π/3) * 2 = -2sin(2x - π/3)
c) y = tan(x^3)
Đặt u = x^3, v = u. Khi đó, y = tan(u). Ta có:
- u' = 3x^2
- v' = 1/cos^2(u)
Vậy, y' = (1/cos^2(x^3)) * 3x^2 = (3x^2)/cos^2(x^3)
d) y = cot(√(x + 1))
Đặt u = √(x + 1), v = u. Khi đó, y = cot(u). Ta có:
- u' = 1/(2√(x + 1))
- v' = -1/sin^2(u)
Vậy, y' = (-1/sin^2(√(x + 1))) * (1/(2√(x + 1))) = -1/(2√(x + 1) * sin^2(√(x + 1))
Lưu ý khi giải bài tập
Khi giải các bài tập về đạo hàm, cần chú ý:
- Xác định đúng hàm số bên trong và hàm số bên ngoài.
- Áp dụng đúng quy tắc đạo hàm của hàm hợp.
- Sử dụng chính xác các công thức đạo hàm cơ bản.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự
Để luyện tập thêm, bạn có thể giải các bài tập tương tự trong SGK Toán 11 tập 2 - Cánh Diều hoặc các đề thi thử Toán 11.
tusach.vn hy vọng với lời giải chi tiết này, bạn sẽ hiểu rõ hơn về cách giải Bài 3 trang 99 SGK Toán 11 tập 2 - Cánh Diều và tự tin hơn trong các bài kiểm tra sắp tới.