Bài 3 trang 100 SGK Toán 11 Tập 1 - Cánh Diều: Giải tích hàm số
Bài 3 thuộc chương trình giải tích hàm số lớp 11, tập trung vào việc xét dấu và lập bảng biến thiên của hàm số bậc hai. Đây là một bài tập quan trọng giúp học sinh nắm vững kiến thức về hàm số và ứng dụng vào giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải khác nhau để giúp bạn hiểu sâu sắc về bài toán này.
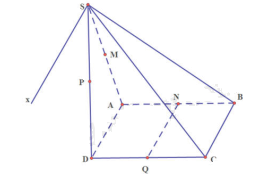
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, AB, SD. Xác định giao tuyến của mỗi cặp mặt phẳng sau: (SAD) và (SBC); (MNP) và (ABCD).
Bài 3 trang 100 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 3 trang 100 SGK Toán 11 Tập 1 - Cánh Diều yêu cầu xét dấu và lập bảng biến thiên của hàm số bậc hai. Để giải bài toán này, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc hai, bao gồm:
- Dạng tổng quát của hàm số bậc hai: y = ax2 + bx + c (a ≠ 0)
- Hệ số a: Xác định chiều mở rộng của parabol (a > 0: mở lên, a < 0: mở xuống)
- Đỉnh của parabol: I(-b/2a, -Δ/4a)
- Trục đối xứng: x = -b/2a
- Nghiệm của phương trình bậc hai: Δ = b2 - 4ac
Hướng dẫn giải bài tập
Để giải Bài 3 trang 100 SGK Toán 11 Tập 1 - Cánh Diều, bạn có thể thực hiện theo các bước sau:
- Xác định hệ số a, b, c của hàm số.
- Tính delta (Δ): Δ = b2 - 4ac
- Xác định dấu của delta (Δ):
- Δ > 0: Hàm số có hai nghiệm phân biệt.
- Δ = 0: Hàm số có nghiệm kép.
- Δ < 0: Hàm số không có nghiệm thực.
- Tìm nghiệm của phương trình bậc hai (nếu Δ ≥ 0): x1 = (-b + √Δ) / 2a và x2 = (-b - √Δ) / 2a
- Xác định khoảng đồng biến, nghịch biến:
- Nếu a > 0: Hàm số nghịch biến trên (-∞; -b/2a) và đồng biến trên (-b/2a; +∞).
- Nếu a < 0: Hàm số đồng biến trên (-∞; -b/2a) và nghịch biến trên (-b/2a; +∞).
- Tìm giá trị của hàm số tại đỉnh: yđỉnh = -Δ/4a
- Lập bảng biến thiên: Dựa vào các thông tin đã tính toán để lập bảng biến thiên của hàm số.
Ví dụ minh họa
Giả sử hàm số cần xét là: y = x2 - 4x + 3
Bước 1: a = 1, b = -4, c = 3
Bước 2: Δ = (-4)2 - 4 * 1 * 3 = 16 - 12 = 4
Bước 3: Δ > 0, hàm số có hai nghiệm phân biệt.
Bước 4: x1 = (4 + √4) / 2 = 3 và x2 = (4 - √4) / 2 = 1
Bước 5: a > 0, hàm số nghịch biến trên (-∞; 2) và đồng biến trên (2; +∞).
Bước 6: yđỉnh = -4 / (4 * 1) = -1
Bước 7: Lập bảng biến thiên (bảng biến thiên sẽ được trình bày dưới dạng bảng).
Lưu ý quan trọng
Khi giải Bài 3 trang 100 SGK Toán 11 Tập 1 - Cánh Diều, bạn cần chú ý đến việc xác định đúng hệ số a, b, c và tính toán chính xác delta (Δ). Việc lập bảng biến thiên cần đảm bảo tính chính xác và đầy đủ các thông tin quan trọng.
Nếu bạn gặp khó khăn trong quá trình giải bài tập, đừng ngần ngại tham khảo các tài liệu tham khảo hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè. tusach.vn luôn sẵn sàng hỗ trợ bạn trong quá trình học tập.