Lý thuyết Hình lăng trụ đứng, hình chóp đều, thể tích của một số hình khối - Toán 11 Cánh diều
Tổng quan nội dung
Lý thuyết Hình lăng trụ đứng, Hình chóp đều - Toán 11 Cánh Diều
Bài viết này cung cấp đầy đủ lý thuyết về hình lăng trụ đứng và hình chóp đều, những kiến thức nền tảng quan trọng trong chương trình Toán 11 Cánh Diều.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, các yếu tố liên quan và đặc biệt là công thức tính thể tích của các hình khối này.
Tusach.vn hy vọng sẽ giúp bạn nắm vững kiến thức và tự tin giải các bài tập liên quan.
1. Hình lăng trụ đứng. Hình lăng trụ đều - Hình lăng trụ có cạnh bên vuông góc với mặt đáy được gọi là hình lăng trụ đứng.
1. Hình lăng trụ đứng. Hình lăng trụ đều
- Hình lăng trụ có cạnh bên vuông góc với mặt đáy được gọi là hình lăng trụ đứng.
- Hình lăng trụ đứng có đáy là đa giác đều gọi là hình lăng trụ đều.
- Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.
Ví dụ: Hình dưới biểu diễn hình lăng trụ đứng tứ giác ABCD.A'B'C'D'.
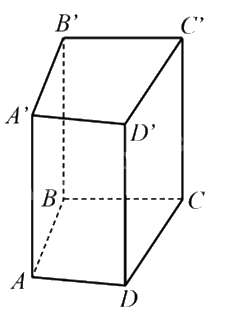
Nhận xét:
- Mỗi mặt bên của hình lăng trụ đứng là một hình chữ nhật, mặt phẳng chứa nó vuông góc với mặt đáy.
- Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.
Hình hộp chữ nhật có 6 mặt là hình chữ nhật.
Nếu mỗi mặt của hình hộp là hình chữ nhật thì hình hộp đó là hình hộp chữ nhật.
Độ dài các đường chéo của hình hộp chữ nhật là bằng nhau.
- Hình lập phương là hình hộp chữ nhật có tất cả các mặt là hình vuông.
Hình lập phương là hình lăng trụ tứ giác đều có cạnh bên bằng cạnh đáy.
2. Hình chóp đều. Hình chóp cụt đều
a) Hình chóp đều
Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
Chú ý:
- Hình chóp tam giác đều có cạnh bên bằng cạnh đáy là tứ diện đều.
- Đoạn thẳng nối đỉnh với hình chiếu của đỉnh trên mặt đáy gọi là đường cao.
Ví dụ: Hình dưới đây biểu diễn hình chóp tứ giác đều S.ABCD.
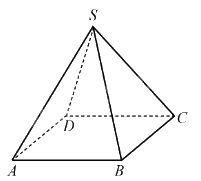
Nhận xét: Chân đường cao của hình chóp đều là tâm đường tròn ngoại tiếp của đáy.
b) Hình chóp cụt đều
Cho hình chóp đều \(S.{A_1}{A_2} \ldots {A_n}\). Mặt phẳng \((P)\) song song với đáy của hình chóp và cắt các cạnh \(S{A_1},S{A_2}, \ldots ,S{A_n}\) lần lượt tại \({B_1},{B_2}, \ldots ,{B_n}\).
Phần của hình chóp đã cho giới hạn bởi hai mặt phẳng \((P)\) và \(\left( {{A_1}{A_2}{A_3} \ldots {A_n}} \right)\) được gọi là hình chóp cụt đều \({A_1}{A_2} \ldots {A_n}{B_1}{B_2} \ldots {B_n}\).
Trong hình chóp cụt đều \({A_1}{A_2} \ldots {A_n} \cdot {B_1}{B_2} \ldots {B_n}\), ta gọi:
- Các đa giác \({A_1}{A_2} \ldots {A_n},{B_1}{B_2} \ldots {B_n}\) lần lượt là đáy lớn, đáy nhỏ;
- Các tứ giác \({A_1}{A_2}{B_2}{B_1},{A_2}{A_3}{B_3}{B_2}, \ldots ,{A_n}{A_1}{B_1}{B_n}\) là các mặt bên;
- Các đoạn thẳng \({A_1}{B_1},{A_2}{B_2}, \ldots ,{A_n}{B_n}\) là các cạnh bên;
- Các cạnh của hai đa giác \({A_1}{A_2} \ldots {A_n},{B_1}{B_2} \ldots {B_n}\) là các cạnh đáy.
Ví dụ: Hình dưới đây biểu diễn hình chóp cụt tứ giác đều \({A_1}{A_2}{A_3}{A_4}.{B_1}{B_2}{B_3}{B_4}\).
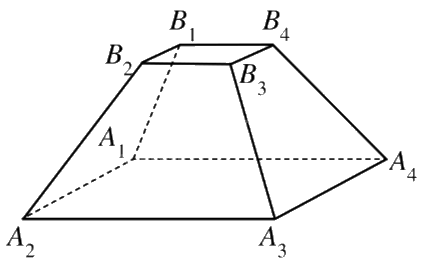
Nhận xét:
- Hai đáy của hình chóp cụt đều nằm trên hai mặt phẳng song song và có các cạnh tương ứng song song; dồng thời hai dáy dó là các da giác dều có củng số cạnh;
- Mỗi mặt bên cùa hình chóp cụt đều là một hình thang cân;
- Các đường thẳng chứa cạnh bên của hình chóp cụt đều cùng đi qua một điểm;
- Đoạn thẳng nối tâm của hai đáy vuông góc với hai đáy của hình chóp cụt đều và gọi là đường cao.
3. Thể tích của một số hình khối
Phần không gian được giới hạn bởi một hình lăng trụ (kể cả hình lăng trụ ấy) được gọi là khối lăng trụ. Các khối khác được định nghĩa tương tự.
a) Thể tích của khối lăng trụ
- Chiều cao của khối lăng trụ bằng khoảng cách giữa hai mặt đáy.
- Thể tích của khối lăng trụ được tính theo công thức:
\(V = Sh{\rm{,}}\)
trong đó \(h\) là chiều cao, \(S\) là diện tích đáy của khối lăng trụ.
b) Thể tích của khối chóp
- Chiều cao của khối chóp bằng khoảng cách từ đỉnh đến mặt đáy.
- Thể tích của khối chóp được tính theo công thức:
\(V = \frac{1}{3}Sh{\rm{, }}\)trong đó \(h\) là chiều cao, \(S\) là diện tích đáy của khối chóp.
c) Thể tích của khối chóp cụt đều
- Chiều cao của khối chóp cụt đều bằng khoảng cách giữa hai mặt đáy.
- Thể tích của khối chóp cụt đều được tính theo công thức:
\(V = \frac{1}{3}h\left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right),\)
trong đó \(h\) là chiều cao và \({S_1},{S_2}\) lần lượt là diện tích hai đáy của khối chóp cụt đều.
Lý Thuyết Hình Lăng Trụ Đứng, Hình Chóp Đều - Toán 11 Cánh Diều
Chào mừng các em học sinh đến với bài học về lý thuyết hình lăng trụ đứng và hình chóp đều trong chương trình Toán 11 Cánh Diều. Đây là một phần quan trọng của chương Hình học không gian, giúp các em hiểu rõ hơn về các hình khối trong không gian ba chiều.
I. Hình Lăng Trụ Đứng
1. Định nghĩa: Hình lăng trụ đứng là hình đa diện có hai mặt đáy song song và bằng nhau, các cạnh bên vuông góc với hai mặt đáy. Các mặt bên là các hình chữ nhật.
2. Các yếu tố của hình lăng trụ đứng:
- Mặt đáy: Hai mặt song song và bằng nhau.
- Mặt bên: Các hình chữ nhật nối các cạnh đáy.
- Chiều cao: Khoảng cách giữa hai mặt đáy.
- Đỉnh: Các điểm trên mặt đáy.
3. Công thức tính thể tích hình lăng trụ đứng:
V = B * h
Trong đó:
- V: Thể tích hình lăng trụ đứng
- B: Diện tích mặt đáy
- h: Chiều cao hình lăng trụ đứng
II. Hình Chóp Đều
1. Định nghĩa: Hình chóp đều là hình đa diện có đáy là một đa giác đều và đỉnh của hình chóp nằm trên đường thẳng vuông góc với tâm của đa giác đáy.
2. Các yếu tố của hình chóp đều:
- Mặt đáy: Đa giác đều.
- Mặt bên: Các tam giác cân bằng nhau.
- Chiều cao: Khoảng cách từ đỉnh đến mặt đáy.
- Đỉnh: Điểm nằm trên đường thẳng vuông góc với tâm đáy.
3. Công thức tính thể tích hình chóp đều:
V = (1/3) * B * h
Trong đó:
- V: Thể tích hình chóp đều
- B: Diện tích mặt đáy
- h: Chiều cao hình chóp đều
III. Bài Tập Minh Họa
Bài 1: Tính thể tích của hình lăng trụ đứng có đáy là hình vuông cạnh 5cm và chiều cao 8cm.
Giải:
Diện tích đáy: B = 5 * 5 = 25 cm2
Thể tích: V = 25 * 8 = 200 cm3
Bài 2: Tính thể tích của hình chóp đều có đáy là hình tam giác đều cạnh 6cm và chiều cao 10cm.
Giải:
Diện tích đáy: B = (62 * √3) / 4 = 9√3 cm2
Thể tích: V = (1/3) * 9√3 * 10 = 30√3 cm3
IV. Lưu Ý Quan Trọng
Khi tính thể tích hình lăng trụ đứng và hình chóp đều, điều quan trọng là phải xác định đúng diện tích mặt đáy và chiều cao của hình. Đơn vị đo phải thống nhất.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức cơ bản và hữu ích về lý thuyết hình lăng trụ đứng và hình chóp đều. Chúc các em học tốt!
| Hình Khối | Công Thức Tính Thể Tích |
|---|---|
| Hình Lăng Trụ Đứng | V = B * h |
| Hình Chóp Đều | V = (1/3) * B * h |
| B: Diện tích đáy, h: Chiều cao | |