Bài 6 trang 100 SGK Toán 11 tập 1 - Cánh diều
Tổng quan nội dung
Bài 6 trang 100 SGK Toán 11 Tập 1 - Cánh Diều: Giải pháp chi tiết
Bài 6 trang 100 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ. a) Chứng minh rằng bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành. b) Chứng minh rằng (IK//BC) c) Xác định giao tuyến của hai mặt phẳng (IJKL) và (SBC)
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ.
a) Chứng minh rằng bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành.
b) Chứng minh rằng \(IK//BC\)
c) Xác định giao tuyến của hai mặt phẳng (IJKL) và (SBC)
Phương pháp giải - Xem chi tiết
Định lý Talet đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Đường trung bình của tam giác:
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Dấu hiệu nhận biết hình bình hành:
Hình có một cặp cạnh đối song song và bằng nhau là hình bình hành.
Lời giải chi tiết
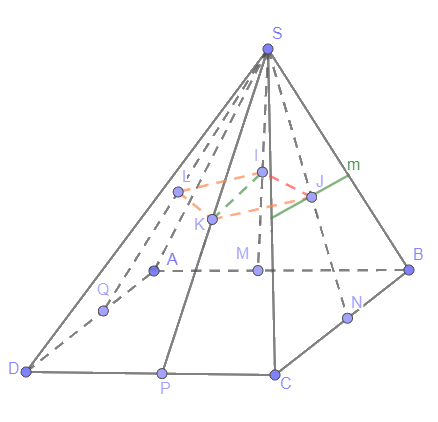
a) Tam giác ABC có M, N là trung điểm của AB, BC nên MN // AC (1)
Tam giác ACD có P, Q là trung điểm của CD, DA nên PQ // AC (2)
Tam giác SMN có I, J là trung điểm của SM, SN nên IJ // MN (3)
Tam giác SPQ có L, K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1), (2), (3), (4) suy ra IJ // LK
Suy ra I, J, K, L đồng phẳng
Ta có:\(\frac{{MN}}{{AC}} = \frac{{QP}}{{AC}} = \frac{1}{2}\)
\(\frac{{{\rm{IJ}}}}{{MN}} = \frac{{LK}}{{PQ}} = \frac{1}{2}\)
Suy ra IJ = LK mà IJ // LK
Suy ra IJKL là hình bình hành
b) Ta có M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
Tam giác SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1) và (2) suy ra: IK // BC
c) Ta có: J là giao điểm của hai mặt phẳng (IJKL) và (SBC)
mà IK // BC
Từ J kẻ Jm // BC
Suy ra Jm là giao tuyến của hai mặt phẳng (IJKL) và (SBC)
Bài 6 trang 100 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 6 trang 100 SGK Toán 11 Tập 1 - Cánh Diều thuộc chương trình học Toán 11, tập trung vào ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Bài tập này không chỉ giúp học sinh củng cố kiến thức lý thuyết mà còn rèn luyện kỹ năng giải toán thực tế.
Nội dung bài tập
Bài 6 yêu cầu học sinh xét hàm số f(x) = x3 - 3x2 + 2 và thực hiện các yêu cầu sau:
- Tìm đạo hàm f'(x).
- Giải phương trình f'(x) = 0.
- Lập bảng biến thiên của hàm số.
- Xác định các điểm cực trị của hàm số.
Lời giải chi tiết
Bước 1: Tìm đạo hàm f'(x)
Sử dụng quy tắc đạo hàm của hàm số đa thức, ta có:
f'(x) = 3x2 - 6x
Bước 2: Giải phương trình f'(x) = 0
Giải phương trình 3x2 - 6x = 0, ta được:
3x(x - 2) = 0
Suy ra x = 0 hoặc x = 2
Bước 3: Lập bảng biến thiên của hàm số
Ta có bảng biến thiên sau:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Bước 4: Xác định các điểm cực trị của hàm số
Dựa vào bảng biến thiên, ta thấy:
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Lưu ý quan trọng
Khi giải bài tập về đạo hàm và cực trị, học sinh cần nắm vững các quy tắc đạo hàm cơ bản và hiểu rõ ý nghĩa của đạo hàm trong việc xác định tính đơn điệu của hàm số. Việc lập bảng biến thiên là một công cụ hữu ích để trực quan hóa sự thay đổi của hàm số và xác định các điểm cực trị.
Ứng dụng của bài tập
Bài tập này có ứng dụng thực tế trong nhiều lĩnh vực, chẳng hạn như:
- Kinh tế: Tìm điểm tối đa lợi nhuận hoặc điểm tối thiểu chi phí.
- Kỹ thuật: Tối ưu hóa thiết kế để đạt hiệu suất cao nhất.
- Khoa học: Nghiên cứu sự thay đổi của các hiện tượng tự nhiên.
Kết luận: Bài 6 trang 100 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ là nền tảng vững chắc cho các bài học tiếp theo.
Nếu bạn gặp khó khăn trong quá trình giải bài tập, đừng ngần ngại tham khảo các tài liệu hỗ trợ hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè. tusach.vn luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục môn Toán!