Bài 2 trang 77 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Bài 2 trang 77 SGK Toán 11 Tập 1 - Cánh Diều
Bài 2 trang 77 SGK Toán 11 Tập 1 - Cánh Diều là bài tập thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng về dãy số, cấp số cộng, cấp số nhân. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
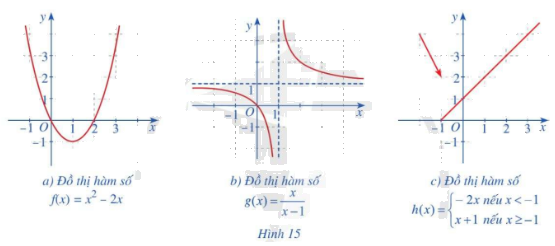
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
Đề bài
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
Phương pháp giải - Xem chi tiết
- Các hàm đa thức liên tục trên \(\mathbb{R}\)
- Các hàm phân thức hữu tỉ liên tục trên từng khoảng xác định của chúng
- Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải chi tiết
+) Hình 15a: Hàm số \(f\left( x \right) = {x^2}\;-2x\) có tập xác định \(D = \mathbb{R}.\)
Hàm số liên tục trên \(\mathbb{R}.\)
+) Hình 15b: Hàm số \(g\left( x \right) = \frac{x}{{x - 1}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;1} \right)\)và \(\left( {1; + \infty } \right).\)
+) Hình 15c:
Với \(x\; \in \;\left( {-\infty ;-1} \right)\) có \(f\left( x \right) = -2x\) liên tục với mọi \(x\; \in \;\left( {-\infty ;-1} \right)\)
Với \(x\; \in \;\left( {-1; + \infty } \right)\) có \(f\left( x \right) = x + 1\) liên tục với mọi \(x\; \in \;\left( {-1; + \infty } \right)\)
Tại x = – 1 có
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \left( {2x} \right) = 2.\left( { - 1} \right) = - 2\\f\left( { - 1} \right) = - 1 + 1 = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - 1} f\left( x \right) \ne f\left( { - 1} \right)\end{array}\)
Do đó hàm số không liên tục tại x = – 1.
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;-1} \right)\)và \(\left( {-1; + \infty } \right).\)
Giải Bài 2 trang 77 SGK Toán 11 Tập 1 - Cánh Diều Chi Tiết
Bài 2 trang 77 SGK Toán 11 Tập 1 - Cánh Diều yêu cầu chúng ta giải quyết các bài toán liên quan đến dãy số, đặc biệt là cấp số cộng và cấp số nhân. Để giải quyết bài tập này một cách hiệu quả, chúng ta cần nắm vững các công thức và tính chất của dãy số.
Nội dung bài tập:
Bài tập thường bao gồm các dạng sau:
- Xác định dãy số: Cho một dãy số, yêu cầu xác định xem đó có phải là cấp số cộng hay cấp số nhân hay không.
- Tìm số hạng tổng quát: Cho biết số hạng đầu và công sai (hoặc công bội), yêu cầu tìm số hạng tổng quát của dãy số.
- Tính tổng các số hạng: Yêu cầu tính tổng của n số hạng đầu tiên của một cấp số cộng hoặc cấp số nhân.
- Ứng dụng vào thực tế: Các bài toán liên quan đến các tình huống thực tế, yêu cầu vận dụng kiến thức về dãy số để giải quyết.
Lời giải chi tiết:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, tusach.vn sẽ trình bày lời giải chi tiết cho từng phần của bài tập.
Ví dụ: (Giả sử bài tập yêu cầu tìm số hạng thứ 10 của một cấp số cộng có số hạng đầu là 2 và công sai là 3)
Lời giải:
- Xác định công thức tổng quát: Số hạng thứ n của cấp số cộng được tính theo công thức: un = u1 + (n-1)d, trong đó u1 là số hạng đầu, d là công sai.
- Áp dụng công thức: Thay u1 = 2, d = 3 và n = 10 vào công thức, ta có: u10 = 2 + (10-1) * 3 = 2 + 9 * 3 = 29
- Kết luận: Vậy số hạng thứ 10 của cấp số cộng là 29.
Mẹo giải nhanh:
Để giải nhanh các bài tập về dãy số, các em nên:
- Nắm vững các công thức và tính chất của cấp số cộng và cấp số nhân.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
Lưu ý quan trọng:
Khi giải bài tập về dãy số, các em cần chú ý:
- Đọc kỹ đề bài để hiểu rõ yêu cầu của bài tập.
- Kiểm tra lại kết quả sau khi giải xong để đảm bảo tính chính xác.
- Nếu gặp khó khăn, hãy tham khảo lời giải chi tiết trên tusach.vn hoặc hỏi thầy cô giáo.
tusach.vn hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên, các em học sinh sẽ tự tin hơn khi giải Bài 2 trang 77 SGK Toán 11 Tập 1 - Cánh Diều và đạt kết quả tốt trong môn Toán.
Ngoài ra, các bạn có thể tham khảo thêm các bài giải khác của SGK Toán 11 Tập 1 - Cánh Diều tại tusach.vn để nâng cao kiến thức và kỹ năng giải toán.