Bài 14 Trang 56 Toán 11 Tập 2 - Cánh Diều | Giải Chi Tiết & Chính Xác

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều: Giải tích

Bài 14 thuộc chương trình giải tích lớp 11, tập trung vào việc ôn tập về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập Toán 11.

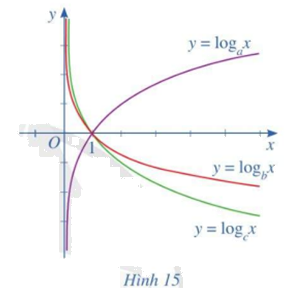
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit (y = {log _a}x;,y = {log _b}x;,y = {log _c}x) được cho bởi Hình 15.

Đề bài

Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều 1

A. c < a < b

B. c < b < a

C. a < b < c

D. b < c < a

Phương pháp giải - Xem chi tiết Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều 2

Dựa vào các hệ số và tính đồng biến, nghịch biến của hàm số lôgarit để suy ra

Lời giải chi tiết

- Do \(y = {\log _a}x\) đồng biến => a lớn nhất => Loại A, C

- Do \({\log _b}x > {\log _c}x\) theo đồ thị. Mà \(y = {\log _b}x;\,y = {\log _c}x\) nghịch biến nê b < c => Chọn D

Bài 14 Trang 56 Toán 11 Tập 2 - Cánh Diều: Giải Chi Tiết và Hướng Dẫn

Bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Bài tập này thường yêu cầu học sinh thực hiện các bước như tính đạo hàm, tìm cực trị, và khảo sát hàm số. Dưới đây là giải chi tiết bài 14, cùng với những hướng dẫn hữu ích để bạn có thể tự giải bài tập một cách hiệu quả.

Nội dung bài tập

Bài 14 thường bao gồm các câu hỏi liên quan đến:

Tính đạo hàm của hàm số.
Tìm các điểm cực trị của hàm số.
Khảo sát sự biến thiên của hàm số.
Vẽ đồ thị hàm số.

Giải chi tiết bài 14 trang 56

Để giải bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều, bạn cần thực hiện theo các bước sau:

Bước 1: Xác định hàm số. Đọc kỹ đề bài để xác định chính xác hàm số cần khảo sát.
Bước 2: Tính đạo hàm cấp một. Sử dụng các quy tắc tính đạo hàm để tìm đạo hàm cấp một của hàm số.
Bước 3: Tìm các điểm cực trị. Giải phương trình đạo hàm cấp một bằng 0 để tìm các điểm cực trị.
Bước 4: Lập bảng biến thiên. Dựa vào đạo hàm cấp một và các điểm cực trị, lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến của hàm số.
Bước 5: Khảo sát giới hạn và tiệm cận. Tính giới hạn của hàm số khi x tiến tới vô cùng và các giá trị đặc biệt để xác định tiệm cận.
Bước 6: Vẽ đồ thị hàm số. Dựa vào bảng biến thiên và các thông tin đã tìm được, vẽ đồ thị hàm số.

Ví dụ minh họa

Giả sử hàm số cần khảo sát là y = x³ - 3x² + 2. Ta thực hiện các bước như sau:

Đạo hàm cấp một: y' = 3x² - 6x
Tìm điểm cực trị: 3x² - 6x = 0 => x = 0 hoặc x = 2
Lập bảng biến thiên: (Bảng biến thiên sẽ được trình bày chi tiết hơn với các khoảng đồng biến, nghịch biến và giá trị cực trị)
Khảo sát giới hạn: lim_x→∞ y = ∞ và lim_x→-∞ y = -∞
Vẽ đồ thị: (Đồ thị hàm số sẽ được mô tả dựa trên các thông tin đã tìm được)

Mẹo giải bài tập

Nắm vững các quy tắc tính đạo hàm.
Sử dụng bảng biến thiên để xác định khoảng đồng biến, nghịch biến một cách nhanh chóng.
Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số.

Tài liệu tham khảo

Ngoài SGK Toán 11 tập 2 - Cánh Diều, bạn có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 11.
Các trang web học Toán trực tuyến.
Các video hướng dẫn giải bài tập Toán 11 trên YouTube.

tusach.vn hy vọng với giải chi tiết và hướng dẫn trên, bạn sẽ tự tin giải quyết bài 14 trang 56 SGK Toán 11 tập 2 - Cánh Diều một cách hiệu quả. Chúc bạn học tốt!