Giải mục 4 trang 27, 28, 29 SGK Toán 11 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết mục 4 trang 27, 28, 29 SGK Toán 11 tập 1 - Cánh Diều trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với đội ngũ giáo viên giàu kinh nghiệm, tusach.vn sẽ cung cấp cho các em những lời giải chính xác, dễ hiểu, cùng với các phương pháp giải bài tập hiệu quả.
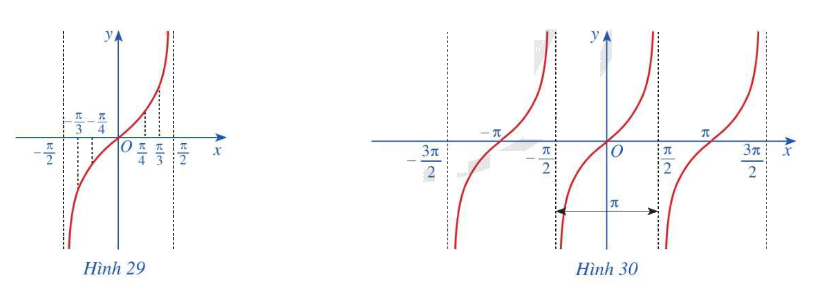
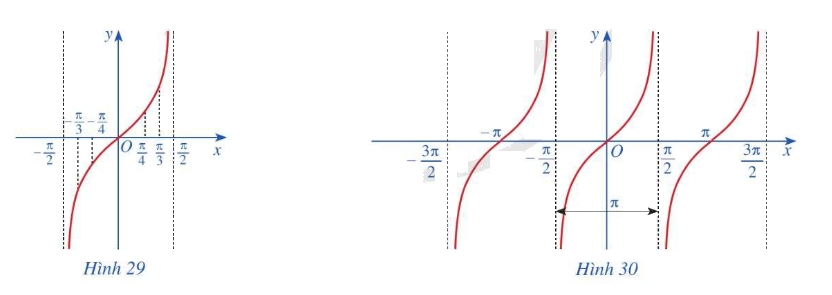
Xét tập hợp (D = mathbb{R}backslash left{ {frac{pi }{2} + kpi |,k in mathbb{Z}} right}). Với mỗi số thực (x in D), hãy nêu định nghĩa (tan x)
Giải mục 4 trang 27, 28, 29 SGK Toán 11 tập 1 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 4 trong SGK Toán 11 tập 1 - Cánh Diều tập trung vào việc nghiên cứu về véc tơ trong không gian. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học toán ở các lớp trên. Việc nắm vững các khái niệm, tính chất và ứng dụng của véc tơ trong không gian là điều cần thiết để giải quyết các bài toán hình học không gian một cách hiệu quả.
Nội dung chính của Mục 4
- Khái niệm véc tơ trong không gian: Định nghĩa, các yếu tố của véc tơ, cách biểu diễn véc tơ.
- Các phép toán véc tơ: Phép cộng, phép trừ, phép nhân với một số thực.
- Tích vô hướng của hai véc tơ: Định nghĩa, tính chất, ứng dụng trong việc tính góc giữa hai véc tơ, kiểm tra tính vuông góc.
- Tích có hướng của hai véc tơ: Định nghĩa, tính chất, ứng dụng trong việc tính diện tích hình bình hành, thể tích hình hộp.
- Ứng dụng của véc tơ trong không gian: Giải các bài toán hình học không gian, chứng minh các đẳng thức véc tơ.
Giải chi tiết các bài tập trang 27, 28, 29
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 4 trang 27, 28, 29 SGK Toán 11 tập 1 - Cánh Diều:
Bài 1: (Trang 27)
Đề bài: Cho hai điểm A(1; 2; 3) và B(3; 4; 5). Tìm tọa độ của véc tơ AB.
Lời giải: Véc tơ AB có tọa độ là (3-1; 4-2; 5-3) = (2; 2; 2).
Bài 2: (Trang 28)
Đề bài: Cho hai véc tơ a = (1; -2; 3) và b = (2; 1; -1). Tính tích vô hướng của a và b.
Lời giải: Tích vô hướng của a và b là a.b = (1*2) + (-2*1) + (3*-1) = 2 - 2 - 3 = -3.
Bài 3: (Trang 29)
Đề bài: Cho ba điểm A(1; 0; 0), B(0; 1; 0) và C(0; 0; 1). Tính diện tích tam giác ABC.
Lời giải: Ta có véc tơ AB = (-1; 1; 0) và véc tơ AC = (-1; 0; 1). Tích có hướng của AB và AC là:
AB x AC = (1*1 - 0*0; 0*(-1) - (-1)*1; (-1)*0 - 1*(-1)) = (1; 1; 1).
Diện tích tam giác ABC là: S = 1/2 * ||AB x AC|| = 1/2 * √(1^2 + 1^2 + 1^2) = 1/2 * √3 = √3 / 2.
Mẹo giải bài tập véc tơ trong không gian
- Nắm vững định nghĩa và tính chất: Đây là nền tảng để giải quyết mọi bài toán.
- Sử dụng công thức một cách chính xác: Kiểm tra lại công thức trước khi áp dụng.
- Vẽ hình minh họa: Giúp hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải các bài tập về véc tơ trong không gian. Chúc các em học tập tốt!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.