Bài 1 trang 14 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Bài 1 trang 14 SGK Toán 11 Tập 2 - Cánh Diều: Giải pháp chi tiết
Bài 1 trang 14 SGK Toán 11 Tập 2 - Cánh Diều là bài tập thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Mẫu số liệu dưới đây ghi lại tốc độ của 40 ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h):
Đề bài
Mẫu số liệu dưới đây ghi lại tốc độ của 40 ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h):

a) Lập bảng tần số ghép nhóm cho mẫu số liệu trên có sáu nhóm ứng với sáu nửa khoảng:
[40 ; 45); [45 ; 50); [50 ; 55); [55 ; 60); [60 ; 65): [65 ; 70)
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
c) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?
Phương pháp giải - Xem chi tiết
- Lần lượt đếm số lượng của từng nhóm để lập bảng
- Áp dụng các công thức vừa được học để xác định các đại lượng tiêu biểu
Lời giải chi tiết
a) Bảng tần số ghép nhóm cho mẫu số liệu trên có sáu nhóm ứng với sáu nửa khoảng:
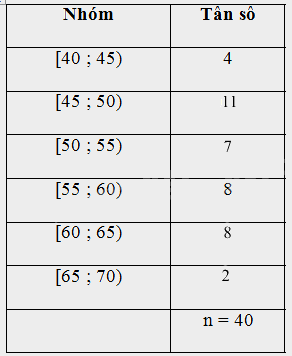
a) Bảng tần số ghép nhóm bao gồm giá trị đại diện và tần số tích lũy:
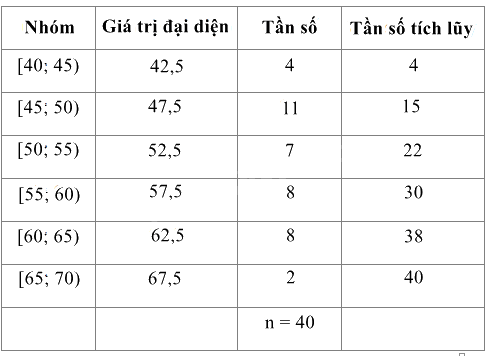
Số phần tử của mẫu là: n = 40
Các đại lượng:
- Số trung bình cộng:
\(\overline x = \frac{{42,5.4 + 47,5.11 + 52,5.7 + 57,5.8 + 62,5.8 + 67,5.2}}{{40}} = 53,875\)
- Trung vị:
\({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 50 + \left( {\frac{{\frac{40}{2} - 15}}{7}} \right).5 \approx 53,6\)
- Tứ phân vị:
+ Tứ phân vị thứ hai: \({Q_2} = {M_e} \approx 53,6\)
+ Tứ phân vị thứ nhất:
\({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 45 + \left( {\frac{{\frac{40}{4} - 4}}{{11}}} \right).5 \approx 47,7\)
+ Tứ phân vị thứ ba:
\(Q = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 55 + \left( {\frac{{\frac{3.40}{4} - 22}}{8}} \right).5 = 60\)
b) Mốt của mẫu số liệu:
\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 45 + \left( {\frac{{11 - 4}}{{2.11 - 4 - 7}}} \right).5 \approx 48,2\)
Bài 1 trang 14 SGK Toán 11 Tập 2 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 1 trang 14 SGK Toán 11 Tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về giới hạn của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 1 yêu cầu học sinh tính các giới hạn sau:
- lim (x→2) (x² - 3x + 2) / (x - 2)
- lim (x→-1) (x³ + 1) / (x + 1)
- lim (x→0) (√(x+1) - 1) / x
Lời giải chi tiết
1. lim (x→2) (x² - 3x + 2) / (x - 2)
Ta có thể phân tích tử thức thành (x - 1)(x - 2). Khi đó:
lim (x→2) (x² - 3x + 2) / (x - 2) = lim (x→2) (x - 1)(x - 2) / (x - 2) = lim (x→2) (x - 1) = 2 - 1 = 1
2. lim (x→-1) (x³ + 1) / (x + 1)
Ta có thể phân tích tử thức thành (x + 1)(x² - x + 1). Khi đó:
lim (x→-1) (x³ + 1) / (x + 1) = lim (x→-1) (x + 1)(x² - x + 1) / (x + 1) = lim (x→-1) (x² - x + 1) = (-1)² - (-1) + 1 = 1 + 1 + 1 = 3
3. lim (x→0) (√(x+1) - 1) / x
Để tính giới hạn này, ta có thể nhân cả tử và mẫu với liên hợp của tử thức là (√(x+1) + 1):
lim (x→0) (√(x+1) - 1) / x = lim (x→0) [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)] = lim (x→0) (x + 1 - 1) / [x(√(x+1) + 1)] = lim (x→0) x / [x(√(x+1) + 1)] = lim (x→0) 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2
Lưu ý khi giải bài tập về giới hạn
- Luôn kiểm tra xem có thể phân tích tử thức hoặc mẫu thức để rút gọn biểu thức hay không.
- Sử dụng các công thức giới hạn cơ bản để đơn giản hóa bài toán.
- Khi gặp dạng vô định, hãy nhân cả tử và mẫu với liên hợp của biểu thức chứa căn thức.
Ứng dụng của kiến thức về giới hạn
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học, đặc biệt là trong việc tính đạo hàm, tích phân và nghiên cứu sự hội tụ của dãy số, chuỗi số. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các môn Toán cao cấp hơn.
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh có thể tự tin giải Bài 1 trang 14 SGK Toán 11 Tập 2 - Cánh Diều và các bài tập tương tự. Chúc các bạn học tốt!