Bài 4 trang 104 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Bài 4 trang 104 SGK Toán 11 Tập 1 - Cánh Diều
Bài 4 thuộc chương trình học Toán 11 Tập 1, sách Cánh Diều, tập trung vào việc rèn luyện kỹ năng về phép biến hóa lượng giác và ứng dụng trong giải toán. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng đường thẳng MN song song với giao tuyến d của hai mặt phẳng (SBC) và (SAD).
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng đường thẳng MN song song với giao tuyến d của hai mặt phẳng (SBC) và (SAD).
Phương pháp giải - Xem chi tiết
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a
Lời giải chi tiết
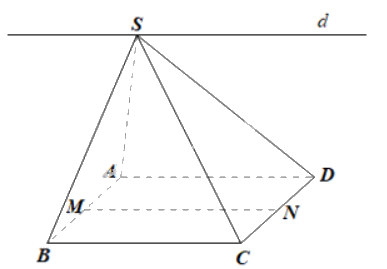
Ta có: S ∈ (SAD) và S ∈ (SBC) nên S là giao điểm của (SAD) và (SBC).
Lại có: AD // BC (do ABCD là hình bình hành);
AD ⊂ (SAD);
BC ⊂ (SBC).
Do đó giao tuyến d của hai mặt phẳng (SAD) và (SBC) là đường thẳng đi qua S và song song với AD, BC.
Vì M, N lần lượt là trung điểm của AB và CD nên MN là đường trung bình
Do đó MN // BC // AD.
Ta có: MN // BC mà BC ⊂ (SBC) nên MN // (SBC);
MN // AD mà AD ⊂ (SAD) nên MN // (SAD).
Có: MN // (SBC);
MN // (SAD);
(SAD) ∩ (SBC) = d
Suy ra MN // d.
Bài 4 trang 104 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 4 trang 104 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về phép biến hóa lượng giác. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này, được cung cấp bởi tusach.vn.
Nội dung bài tập
Bài 4 yêu cầu học sinh thực hiện các phép biến đổi lượng giác để rút gọn biểu thức hoặc chứng minh đẳng thức. Cụ thể, bài tập thường bao gồm các dạng sau:
- Rút gọn biểu thức lượng giác sử dụng các công thức biến đổi.
- Chứng minh đẳng thức lượng giác bằng cách biến đổi vế này thành vế kia.
- Giải phương trình lượng giác cơ bản.
Lời giải chi tiết
Để giải bài 4 trang 104 SGK Toán 11 Tập 1 - Cánh Diều, bạn cần nắm vững các công thức lượng giác cơ bản như:
- Công thức cộng và hiệu góc: sin(a ± b), cos(a ± b), tan(a ± b), cot(a ± b)
- Công thức nhân đôi: sin(2a), cos(2a), tan(2a), cot(2a)
- Công thức hạ bậc: sin2(a), cos2(a), tan2(a), cot2(a)
Dưới đây là ví dụ về cách giải một dạng bài tập thường gặp:
Ví dụ: Rút gọn biểu thức
Rút gọn biểu thức: A = sin2(x) + cos2(x) + 2sin(x)cos(x)
Lời giải:
- Áp dụng công thức sin2(x) + cos2(x) = 1
- Áp dụng công thức sin(2x) = 2sin(x)cos(x)
- Thay vào biểu thức A, ta có: A = 1 + sin(2x)
Mẹo giải bài tập
Để giải bài tập về phép biến hóa lượng giác hiệu quả, bạn nên:
- Nắm vững các công thức lượng giác cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công thức biến đổi một cách linh hoạt để rút gọn biểu thức hoặc chứng minh đẳng thức.
- Kiểm tra lại kết quả sau khi giải bài tập.
Tài liệu tham khảo thêm
Ngoài SGK Toán 11 Tập 1 - Cánh Diều, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán:
- Sách bài tập Toán 11
- Các trang web học Toán trực tuyến như tusach.vn
- Các video bài giảng Toán 11 trên YouTube
Kết luận
Bài 4 trang 104 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng, giúp học sinh rèn luyện kỹ năng về phép biến hóa lượng giác. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các bạn học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
Hãy truy cập tusach.vn để xem thêm nhiều bài giải Toán 11 Tập 1 - Cánh Diều và các tài liệu học tập hữu ích khác!