Lý thuyết Đường thẳng và mặt phẳng song song - SGK Toán 11 Cánh Diều
Tổng quan nội dung
Lý thuyết Đường thẳng và Mặt phẳng song song - Toán 11 Cánh Diều
Chào mừng bạn đến với bài học lý thuyết quan trọng trong chương trình Hình học không gian lớp 11! Bài viết này sẽ cung cấp đầy đủ và chi tiết kiến thức về đường thẳng và mặt phẳng song song, dựa trên nội dung sách giáo khoa Toán 11 Cánh Diều.
Chúng ta sẽ cùng nhau khám phá các định nghĩa, tính chất, điều kiện nhận biết và ứng dụng của các khái niệm này. Tusach.vn cam kết mang đến cho bạn trải nghiệm học tập hiệu quả và thú vị.
I. Đường thẳng song song với mặt phẳng
I. Đường thẳng song song với mặt phẳng
Đường thẳng được gọi là song song với mặt phẳng nếu chúng không có điểm chung.
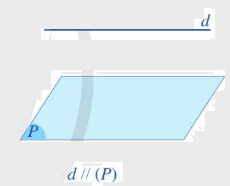
*Nhận xét:
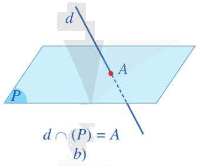
- Nếu d và \(\left( P \right)\) có một điểm chung duy nhất thì ta nói d và \(\left( P \right)\) cắt nhau tại A. Kí hiệu \(d \cap \left( P \right) = A\)hay \(d \cap \left( P \right) = \left\{ A \right\}\).
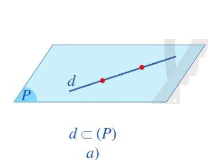
- Nếu d và \(\left( P \right)\) có nhiều hơn 1 điểm chung thì ta nói d nằm trong \(\left( P \right)\) hay \(\left( P \right)\) chứa d. Kí hiệu \(d \subset \left( P \right)\)hay \(\left( P \right) \supset d\).
II. Điều kiện và tính chất
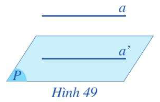
- Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với một đường thẳng a’ nằm trong (P) thì ta nói \(a//\left( P \right)\).
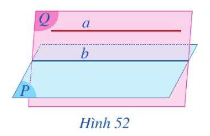
- Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b//a.
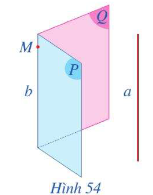
- Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
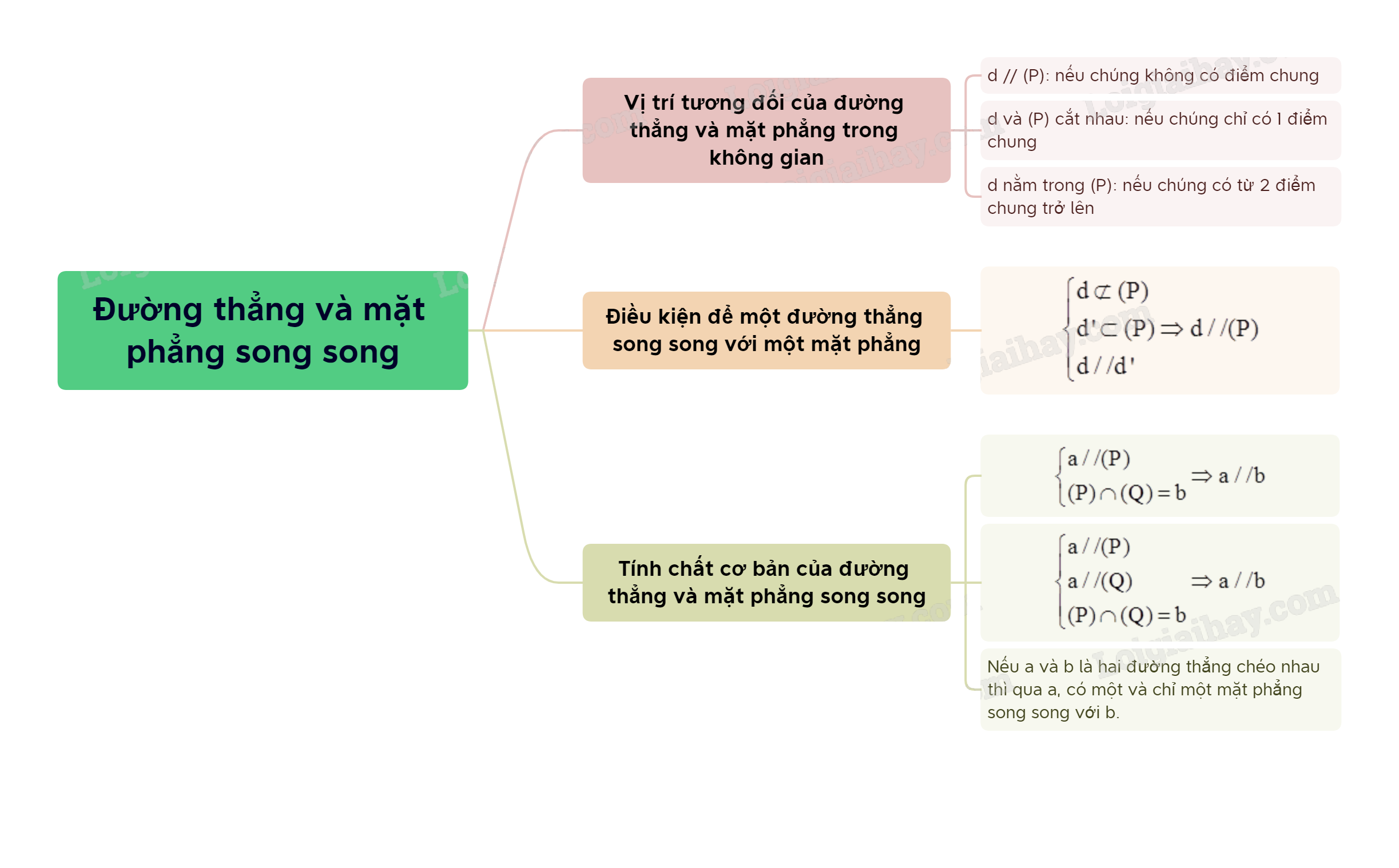
Lý Thuyết Đường Thẳng và Mặt Phẳng Song Song - SGK Toán 11 Cánh Diều: Tổng Quan Chi Tiết
Chương trình Hình học không gian lớp 11 đặt nền móng cho việc hiểu sâu hơn về không gian ba chiều. Một trong những chủ đề quan trọng nhất là lý thuyết về đường thẳng và mặt phẳng song song. Bài viết này sẽ đi sâu vào các khái niệm, định lý, và ứng dụng thực tế của chủ đề này, dựa trên sách giáo khoa Toán 11 Cánh Diều.
1. Định Nghĩa và Các Khái Niệm Cơ Bản
Để hiểu rõ về đường thẳng và mặt phẳng song song, chúng ta cần nắm vững các định nghĩa sau:
- Đường thẳng song song: Hai đường thẳng được gọi là song song nếu chúng không có điểm chung và nằm trong cùng một mặt phẳng.
- Mặt phẳng song song: Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung.
- Đường thẳng song song với mặt phẳng: Một đường thẳng được gọi là song song với một mặt phẳng nếu nó không có điểm chung với mặt phẳng đó.
2. Điều Kiện Nhận Biết Đường Thẳng Song Song với Mặt Phẳng
Có một số điều kiện để nhận biết một đường thẳng song song với một mặt phẳng:
- Nếu đường thẳng đó song song với một đường thẳng nào đó nằm trong mặt phẳng.
- Nếu đường thẳng đó song song với mặt phẳng và không nằm trong mặt phẳng đó.
3. Tính Chất Quan Trọng
Một trong những tính chất quan trọng nhất liên quan đến đường thẳng và mặt phẳng song song là:
Nếu một mặt phẳng chứa một đường thẳng song song với một đường thẳng nằm trong một mặt phẳng khác, thì hai mặt phẳng đó song song.
4. Ứng Dụng của Lý Thuyết
Lý thuyết về đường thẳng và mặt phẳng song song có nhiều ứng dụng trong thực tế, ví dụ:
- Kiến trúc: Trong thiết kế kiến trúc, việc đảm bảo các mặt phẳng và đường thẳng song song là rất quan trọng để tạo ra các công trình ổn định và thẩm mỹ.
- Kỹ thuật: Trong kỹ thuật, lý thuyết này được sử dụng để thiết kế các bộ phận máy móc và các cấu trúc khác.
- Hình học không gian: Nền tảng cho việc giải các bài toán phức tạp hơn về hình học không gian.
5. Bài Tập Vận Dụng (Ví dụ)
Bài tập: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh CD. Chứng minh rằng đường thẳng SM song song với mặt phẳng (ABD).
Hướng dẫn:
- Tìm giao điểm của đường thẳng CM và mặt phẳng (ABD).
- Chứng minh rằng đường thẳng SM song song với đường thẳng CM.
- Kết luận SM song song với mặt phẳng (ABD).
6. Mở Rộng và Liên Hệ
Lý thuyết về đường thẳng và mặt phẳng song song là bước đệm quan trọng để học các khái niệm phức tạp hơn trong hình học không gian, như góc giữa đường thẳng và mặt phẳng, khoảng cách giữa đường thẳng và mặt phẳng, và thể tích hình chóp.
7. Tài Liệu Tham Khảo Thêm
Để hiểu sâu hơn về chủ đề này, bạn có thể tham khảo thêm:
- Sách giáo khoa Toán 11 Cánh Diều
- Các trang web học toán uy tín như tusach.vn
- Các video bài giảng trực tuyến
Tusach.vn hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và đầy đủ về lý thuyết Đường thẳng và Mặt phẳng song song - SGK Toán 11 Cánh Diều. Chúc bạn học tập tốt!