Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải mục 2 trang 51, 52, 53 SGK Toán 11 tập 2 - Cánh Diều
SGK Toán 11 - Cánh diều
Giải Toán 11 tập 2 - Cánh Diều
Chương VI. Hàm số mũ và hàm số lôgarit
Bài 4. Phương trình mũ, bất phương trình mũ và lôgarit

Giải mục 2 trang 51, 52, 53 SGK Toán 11 tập 2 - Cánh Diều

Giải mục 2 trang 51, 52, 53 SGK Toán 11 tập 2 - Cánh Diều

Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 51, 52, 53 sách giáo khoa Toán 11 tập 2 chương trình Cánh Diều. Bài giải được trình bày rõ ràng, logic, giúp học sinh dễ dàng tiếp thu kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cố gắng cung cấp những tài liệu học tập chất lượng nhất, hỗ trợ học sinh học tập hiệu quả.

Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số mũ (y = {left( {frac{1}{2}} right)^x}).

HĐ 5LT 5LT 6HĐ 6LT 7LT 8

HĐ 5

    Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, hãy tìm x sao cho \({\left( {\frac{1}{2}} \right)^x} > 2\)

    Giải mục 2 trang 51, 52, 53 SGK Toán 11 tập 2 - Cánh Diều 1

    Phương pháp giải:

    Dựa vào nhìn đồ thị để xét tính đồng biến nghịch biến

    Lời giải chi tiết:

    - Hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) nghịch biến trên toàn R

    - Dựa vào đồ thị ta thấy: \({\left( {\frac{1}{2}} \right)^x} > 2 \Leftrightarrow x > - 1\)

    LT 5

      Cho hai ví dụ về bất phương trình mũ cơ bản

      Phương pháp giải:

      Dựa vào định nghĩa bất phương trình mũ để xác định

      Lời giải chi tiết:

      Ví dụ:

      + \({3^x} = 9\)

      + \({4^{x + 2}} = 16\)

      LT 6

        Giải mỗi bất phương trình sau:

        a) \({7^{x + 3}} < 343\)

        b) \({\left( {\frac{1}{4}} \right)^x} \ge 3\)

        Phương pháp giải:

        Dựa vào ví dụ 10 để làm

        Lời giải chi tiết:

        a) \({7^{x + 3}} < 343\)

        \(\begin{array}{l} \Leftrightarrow x + 3 < {\log _7}343\\ \Leftrightarrow x + 3 < 3\\ \Leftrightarrow x < 0\end{array}\)

        Vậy tập nghiệm của bất phương trình là: \(\left( { - \infty ;0} \right)\)

        b) \({\left( {\frac{1}{4}} \right)^x} \ge 3\)

        \( \Leftrightarrow x \le {\log _{\frac{1}{4}}}3\)

        Vậy tập nghiệm của bất phương trình là: \(\left( { - \infty ;{{\log }_{\frac{1}{4}}}3} \right]\)

        HĐ 6

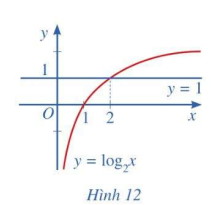
          Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit \(y = {\log _2}x\). Từ đó, hãy tìm x sao cho \({\log _2}x > 1\)

          Giải mục 2 trang 51, 52, 53 SGK Toán 11 tập 2 - Cánh Diều 1

          Phương pháp giải:

          Dựa vào nhìn đồ thị để xét tính đồng biến nghịch biến

          Lời giải chi tiết:

          - Hàm số \(y = {\log _2}x\) đồng biến trên tập xác định

          - Dựa vào đồ thị ta thấy: \({\log _2}x > 1 \Leftrightarrow x > 2\)

          LT 7

            Cho hai ví dụ về bất phương trình logarit cơ bản

            Phương pháp giải:

            Dựa vào định nghĩa để làm

            Lời giải chi tiết:

            1. \(\log x > 1\)
            2. \({\log _3}\left( {x + 1} \right) < 6\)

            LT 8

              Giải mỗi bất phương trình sau:

              a) \({\log _3}x < 2\)

              b) \({\log _{\frac{1}{4}}}\left( {x - 5} \right) \ge - 2\)

              Phương pháp giải:

              Dựa vào ví dụ 13 để làm

              Lời giải chi tiết:

              a) \({\log _3}x < 2\)

              \(\begin{array}{l} \Leftrightarrow 0 < x < {3^2}\\ \Leftrightarrow 0 < x < 9\end{array}\)

              Vậy tập nghiệm của bất phương trình là (0 ; 9)

              b) \({\log _{\frac{1}{4}}}\left( {x - 5} \right) \ge - 2\)

              \(\begin{array}{l} \Leftrightarrow 0 < x - 5 \le {\left( {\frac{1}{4}} \right)^{ - 2}}\\ \Leftrightarrow 5 < x \le 21\end{array}\)

              Vậy tập nghiệm của bất phương trình là \(\left( {5;21} \right]\)

              Giải mục 2 trang 51, 52, 53 SGK Toán 11 tập 2 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết

              Mục 2 của SGK Toán 11 tập 2 - Cánh Diều tập trung vào các kiến thức về Đường thẳng vuông góc với mặt phẳng. Đây là một phần quan trọng trong chương trình hình học không gian, đòi hỏi học sinh phải nắm vững các định nghĩa, tính chất và phương pháp chứng minh liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2, trang 51, 52, 53, giúp các em học sinh hiểu rõ hơn về nội dung bài học và rèn luyện kỹ năng giải toán.

              Nội dung chính của Mục 2:

              • Định nghĩa đường thẳng vuông góc với mặt phẳng: Hiểu rõ điều kiện để một đường thẳng được xem là vuông góc với một mặt phẳng.
              • Tính chất của đường thẳng vuông góc với mặt phẳng: Nắm vững các tính chất quan trọng, ví dụ như đường thẳng vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
              • Điều kiện để đường thẳng vuông góc với mặt phẳng: Biết cách chứng minh một đường thẳng vuông góc với một mặt phẳng dựa trên các điều kiện cho trước.
              • Ứng dụng của đường thẳng vuông góc với mặt phẳng: Giải các bài toán thực tế liên quan đến việc xác định góc giữa đường thẳng và mặt phẳng, tính khoảng cách từ một điểm đến mặt phẳng.

              Giải chi tiết các bài tập trang 51, 52, 53

              Bài 1: (Trang 51)

              (Nội dung bài tập và lời giải chi tiết sẽ được trình bày tại đây. Ví dụ: Bài 1 yêu cầu chứng minh một đường thẳng vuông góc với một mặt phẳng. Lời giải sẽ bao gồm các bước chứng minh cụ thể, sử dụng các định nghĩa và tính chất đã học.)

              Bài 2: (Trang 52)

              (Nội dung bài tập và lời giải chi tiết sẽ được trình bày tại đây. Ví dụ: Bài 2 yêu cầu tính góc giữa một đường thẳng và một mặt phẳng. Lời giải sẽ bao gồm các bước tính toán cụ thể, sử dụng các công thức và định lý liên quan.)

              Bài 3: (Trang 53)

              (Nội dung bài tập và lời giải chi tiết sẽ được trình bày tại đây. Ví dụ: Bài 3 yêu cầu tìm tập hợp các điểm thỏa mãn một điều kiện nào đó liên quan đến đường thẳng vuông góc với mặt phẳng. Lời giải sẽ bao gồm các bước phân tích và suy luận logic để tìm ra tập hợp điểm cần tìm.)

              Mẹo giải toán hiệu quả

              1. Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và các điều kiện cần tìm.
              2. Vẽ hình minh họa: Vẽ hình giúp bạn hình dung rõ hơn về bài toán và tìm ra các mối liên hệ giữa các yếu tố.
              3. Sử dụng các định nghĩa và tính chất: Áp dụng các định nghĩa, tính chất và công thức đã học để giải bài toán.
              4. Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

              Tài liệu tham khảo thêm

              Để hiểu sâu hơn về nội dung bài học, các em có thể tham khảo thêm các tài liệu sau:

              • Sách giáo khoa Toán 11 tập 2 - Cánh Diều
              • Sách bài tập Toán 11 tập 2 - Cánh Diều
              • Các trang web học toán trực tuyến uy tín

              Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán 11. Chúc các em thành công!

              Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

              CHỦ ĐỀ SÁCH XEM NHIỀU

              Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

              VỀ TUSACH.VN