Giải mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Giải mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em.
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P).
Hoạt động 5
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P). Quan sát Hình 19 và cho biết:
a) Nếu hai đường thẳng a và b song song với nhau và mặt phẳng (P) vuông góc với đường thẳng a thì mặt phẳng (P) có vuông góc với đường thẳng b hay không?
b) Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng (P) thì chúng có song song với nhau hay không?
Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
a, Gọi (Q) là mặt phẳng chứa đường thẳng a, b
Theo tính chất 2 “Có duy nhất 1 đường thẳng đi qua 1 điểm cho trước và vuông góc với một mặt phẳng cho trước”
b, Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng (P) thì chúng song song với nhau.
Luyện tập - vận dụng 4
Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O. Lấy các điểm A, B thuộc d khác O; các điểm A', B' thuộc (P) thỏa mãn \(AA' \bot (P),\,BB' \bot (P)\). Chứng minh rằng: \(\frac{{AA'}}{{BB'}} = \frac{{OA}}{{OB}}\)
Phương pháp giải:
Sử dụng định lý Thalès: Nếu một đường thẳng song song với một cạnh của tam giác đó và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:

Do \({\rm{AA}}' \bot (P),\,BB' \bot (P) \Rightarrow {\rm{AA' //}}\,{\rm{BB'}}\)
Xét có \({\rm{AA' //}}\,{\rm{BB'}} \Rightarrow \frac{{{\rm{AA}}'}}{{{\rm{BB'}}}} = \frac{{OA}}{{OB}}\) (Định lý Thalès)
Hoạt động 6
Trong Hình 21 , hai mặt sàn của nhà cao tầng và cột trụ bê tông gợi nên hình ảnh hai mặt phẳng (P), (Q) phân biệt và đường thẳng a.

Quan sát Hình 21 và cho biết:
a) Nếu hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng a vuông góc với mặt phẳng (P) thì đường thẳng a có vuông góc với mặt phẳng (Q) hay không?
b) Nếu hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng a thì chúng có song song với nhau hay không?
Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
a) Nếu (P) // (Q) và \(a \bot (P)\) thì \(a \bot (Q)\)
b) Nếu hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng a thì chúng song song với nhau.
Luyện tập - vận dụng 5
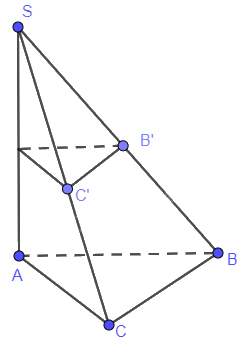
Cho hình chóp S.ABC có SA ⊥ (ABC). Mặt phẳng (P) khác với mặt phẳng (ABC), vuông góc với đường thẳng SA và lần lượt cắt các đường thẳng SB, SC tại hai điểm phân biệt B', C'. Chứng minh rằng B'C' // BC
Phương pháp giải:
Sử dụng tính chất: \(\left\{ \begin{array}{l}(P) \bot a\\(Q) \bot a\end{array} \right. \Rightarrow (P)\,//\,(Q)\)
Lời giải chi tiết:

Do \(\left\{ \begin{array}{l}(P) \bot SA\\(ABC) \bot SA\end{array} \right. \Rightarrow (P)\,//\,(ABC) \Rightarrow B'C'\,//BC\)
Giải mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều: Tổng quan và Phương pháp giải
Mục 4 của SGK Toán 11 tập 2 - Cánh Diều tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Đây là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững các định nghĩa, tính chất và phương pháp chứng minh liên quan. Bài viết này sẽ đi sâu vào việc giải các bài tập trang 83 và 84, cung cấp lời giải chi tiết và dễ hiểu, giúp các em học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán.
Nội dung chính của Mục 4
- Định nghĩa đường thẳng trong không gian: Đường thẳng được xác định bởi một điểm và một vectơ chỉ phương.
- Phương trình tham số của đường thẳng: Dạng phương trình biểu diễn một đường thẳng thông qua một điểm và một vectơ chỉ phương.
- Phương trình chính tắc của đường thẳng: Dạng phương trình biểu diễn một đường thẳng thông qua một điểm và một vectơ chỉ phương, nhưng được viết dưới dạng tỉ lệ.
- Vị trí tương đối của hai đường thẳng trong không gian: Các trường hợp: đồng phẳng (cắt nhau, song song, trùng nhau) và không đồng phẳng.
- Khoảng cách từ một điểm đến một đường thẳng: Công thức tính khoảng cách từ một điểm đến một đường thẳng trong không gian.
Giải chi tiết các bài tập trang 83, 84
Bài 1: (Trang 83)
Đề bài: Cho hai điểm A(1; 2; 3) và B(3; 4; 5). Hãy viết phương trình tham số của đường thẳng AB.
Lời giải:
- Tìm vectơ chỉ phương:AB = (3-1; 4-2; 5-3) = (2; 2; 2). Ta có thể chọn vectơ chỉ phương u = (1; 1; 1).
- Viết phương trình tham số: Phương trình tham số của đường thẳng AB là: x = 1 + ty = 2 + tz = 3 + t
Bài 2: (Trang 84)
Đề bài: Cho đường thẳng d: x = 2 + t, y = 1 - t, z = 3 + 2t và điểm A(1; 0; 2). Hãy tìm tọa độ điểm A' là hình chiếu vuông góc của A lên d.
Lời giải:
Bài toán này đòi hỏi kiến thức về hình chiếu vuông góc và vectơ. (Lời giải chi tiết sẽ được trình bày đầy đủ với các bước tính toán cụ thể, bao gồm việc tìm vectơ pháp tuyến của mặt phẳng vuông góc với d tại A' và giải hệ phương trình để tìm tọa độ A').
Mẹo giải toán hiệu quả
- Nắm vững định nghĩa và tính chất: Đây là nền tảng để giải quyết mọi bài toán.
- Vẽ hình minh họa: Giúp hình dung rõ hơn về bài toán và tìm ra hướng giải.
- Sử dụng công thức một cách chính xác: Kiểm tra lại các công thức trước khi áp dụng.
- Rèn luyện thường xuyên: Làm nhiều bài tập để củng cố kiến thức và kỹ năng.
Kết luận
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh đã hiểu rõ hơn về cách giải các bài tập trong mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều. Hãy tiếp tục luyện tập và áp dụng kiến thức vào các bài tập khác để đạt kết quả tốt nhất. Đừng quên truy cập tusach.vn để tìm kiếm thêm nhiều tài liệu học tập hữu ích khác!