Bài 3 trang 94 Toán 11 Tập 1 - Cánh Diều | Giải chi tiết & Chính xác

Bài 3 trang 94 SGK Toán 11 tập 1 - Cánh diều

Bài 3 trang 94 SGK Toán 11 Tập 1 - Cánh Diều: Giải tích hàm số

Bài 3 thuộc chương trình giải tích hàm số lớp 11, tập trung vào việc xét tính đơn điệu của hàm số. Đây là một phần kiến thức quan trọng giúp học sinh hiểu rõ hơn về đặc điểm và tính chất của các hàm số khác nhau.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu cho từng câu hỏi trong bài, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.

Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy.

Đề bài

Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy.

Phương pháp giải - Xem chi tiết Bài 3 trang 94 SGK Toán 11 tập 1 - Cánh diều 1

Chứng minh giao điểm của ba đường thẳng nằm trên cùng một mặt phẳng, khi đó a, b, c cùng thuộc một mặt phẳng (trái với giả thiết) => giao điểm của ba đường thẳng phải trùng nhau.

Lời giải chi tiết

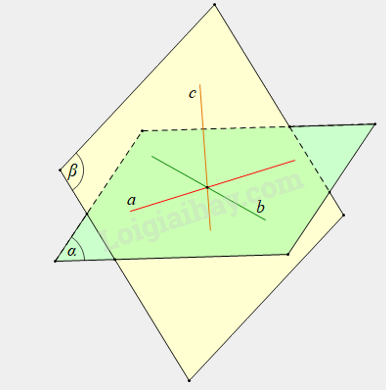
Bài 3 trang 94 SGK Toán 11 tập 1 - Cánh diều 2

Giả sử a ∩ b = {I} và α = mp(a, b);

a ∩ c = {J} và β = mp(a, c);

b ∩ c = {K} và γ = mp(b, c) với các điểm I, J, K phân biệt.

Khi đó α ∩ β = a và đường thẳng a chính là đường thẳng IJ.

α ∩ γ = b và đường thẳng b chính là đường thẳng IK.

β ∩ γ = c và đường thẳng c chính là đường thẳng JK.

Mà chỉ có một mặt phẳng duy nhất đi qua ba điểm I, J, K, đó là (IJK)

Khi đó a, b, c cùng thuộc mặt phẳng (IJK), điều này trái với giả thiết a, b, c không cùng nằm trong một mặt phẳng.

Vậy I, J, K phải trùng nhau hay a, b, c đồng quy.

Bài 3 trang 94 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn

Bài 3 trang 94 SGK Toán 11 Tập 1 - Cánh Diều yêu cầu học sinh xét tính đơn điệu của hàm số. Để giải bài tập này, chúng ta cần nắm vững các kiến thức về đạo hàm và các dấu hiệu để xác định hàm số đồng biến, nghịch biến.

I. Tóm tắt lý thuyết cần nắm vững

Đạo hàm: Đạo hàm của hàm số f(x) tại điểm x, ký hiệu là f'(x), biểu thị tốc độ thay đổi tức thời của hàm số tại điểm đó.
Hàm số đồng biến: Hàm số f(x) được gọi là đồng biến trên khoảng (a, b) nếu với mọi x₁, x₂ thuộc (a, b) và x₁ < x₂ thì f(x₁) < f(x₂). Điều kiện cần và đủ để hàm số f(x) đồng biến trên (a, b) là f'(x) ≥ 0 với mọi x thuộc (a, b).
Hàm số nghịch biến: Hàm số f(x) được gọi là nghịch biến trên khoảng (a, b) nếu với mọi x₁, x₂ thuộc (a, b) và x₁ < x₂ thì f(x₁) > f(x₂). Điều kiện cần và đủ để hàm số f(x) nghịch biến trên (a, b) là f'(x) ≤ 0 với mọi x thuộc (a, b).

II. Giải chi tiết Bài 3 trang 94 SGK Toán 11 Tập 1 - Cánh Diều

Để giải bài tập này, chúng ta sẽ thực hiện các bước sau:

Tính đạo hàm f'(x) của hàm số đã cho.
Xác định dấu của f'(x) trên các khoảng xác định của hàm số.
Kết luận về tính đơn điệu của hàm số dựa vào dấu của f'(x).

Ví dụ: Xét hàm số f(x) = x² - 4x + 3.

Bước 1: Tính đạo hàm: f'(x) = 2x - 4.

Bước 2: Xác định dấu của f'(x):

f'(x) = 0 khi 2x - 4 = 0 => x = 2.
f'(x) > 0 khi x > 2.
f'(x) < 0 khi x < 2.

Bước 3: Kết luận: Hàm số f(x) nghịch biến trên khoảng (-∞, 2) và đồng biến trên khoảng (2, +∞).

III. Luyện tập thêm

Để củng cố kiến thức, các em có thể tự giải thêm các bài tập tương tự trong SGK và sách bài tập Toán 11 Tập 1 - Cánh Diều. Ngoài ra, các em có thể tham khảo các bài giảng trực tuyến và các nguồn tài liệu học tập khác.

IV. Mẹo giải nhanh

Khi xét tính đơn điệu của hàm số, hãy chú ý đến các điểm mà đạo hàm bằng 0 hoặc không xác định. Đây thường là các điểm mấu chốt để xác định khoảng đồng biến, nghịch biến của hàm số.

Tusach.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Bài 3 trang 94 SGK Toán 11 Tập 1 - Cánh Diều và tự tin giải các bài tập tương tự.

Hàm số	Đạo hàm	Tính đơn điệu
f(x) = x²	f'(x) = 2x	Đồng biến trên (0, +∞), nghịch biến trên (-∞, 0)
f(x) = -x²	f'(x) = -2x	Đồng biến trên (-∞, 0), nghịch biến trên (0, +∞)