Bài 5 trang 94 SGK Toán 11 tập 1 - Cánh diều
Tổng quan nội dung
Bài 5 trang 94 SGK Toán 11 Tập 1 - Cánh Diều: Giải tích hàm số
Bài 5 thuộc chương trình giải tích hàm số lớp 11, tập trung vào việc xét dấu và lập bảng biến thiên của hàm số bậc hai. Đây là một bài tập quan trọng giúp học sinh nắm vững kiến thức về hàm số và ứng dụng vào giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải khác nhau để giúp bạn hiểu sâu sắc về bài toán này.
Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,NS = 2NC\) a) Xác định giao điểm của MN với mặt phẳng (ABC) b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC)
Đề bài
Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,NS = 2NC\)
a) Xác định giao điểm của MN với mặt phẳng (ABC)
b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC)
Phương pháp giải - Xem chi tiết
a) Muốn tìm giao điểm của một đường thẳng a và mặt phẳng (P), ta tìm giao điểm của a và một đường thẳng b nằm trong (P):
\(\left\{ \begin{array}{l}a \cap b = M\\b \subset (P)\end{array} \right. \Rightarrow M = a \cap (P)\)
Bước 1: Xác định mp (Q) chứa a
Bước 2: Tìm giao tuyến \(b = (P) \cap (Q)\)
Bước 3: Trong \((Q):a \cap b = M\) mà \(b \subset (P)\)suy ra \(M = a \cap (P)\)
b) Để xác định giao tuyến của hai mặt phẳng, ta tìm điểm chung của chúng.
b, Đường thẳng đi qua hai điểm chung là giao tuyến
Lời giải chi tiết
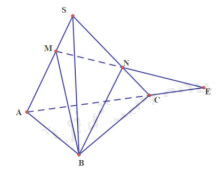
a) Tam giác SAC có: MN cắt AC tại E mà AC thuộc mp (ABC)
Do đó: E là giao điểm của MN và (ABC)
b) Ta có: B thuộc hai mặt phẳng (BMN) và (ABC)
E thuộc hai mặt phẳng (BMN) và (ABC)
Suy ra: BE là giao tuyến của hai mặt phẳng (BMN) và (ABC)
Bài 5 trang 94 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 5 trang 94 SGK Toán 11 Tập 1 - Cánh Diều yêu cầu xét dấu và lập bảng biến thiên của hàm số bậc hai. Để giải bài này, chúng ta cần nắm vững các bước sau:
- Xác định hệ số a, b, c của hàm số: Hàm số bậc hai có dạng y = ax2 + bx + c.
- Tính delta (Δ): Δ = b2 - 4ac.
- Xác định nghiệm của phương trình:
- Nếu Δ > 0: Phương trình có hai nghiệm phân biệt x1, x2.
- Nếu Δ = 0: Phương trình có nghiệm kép x1 = x2 = -b/2a.
- Nếu Δ < 0: Phương trình vô nghiệm.
- Xác định dấu của a:
- Nếu a > 0: Đồ thị hàm số là một parabol hướng lên.
- Nếu a < 0: Đồ thị hàm số là một parabol hướng xuống.
- Lập bảng xét dấu: Dựa vào nghiệm và dấu của a để xét dấu của hàm số trên các khoảng xác định.
- Lập bảng biến thiên: Dựa vào bảng xét dấu để lập bảng biến thiên của hàm số, bao gồm các yếu tố như: x, y, khoảng đồng biến, nghịch biến, cực trị.
Ví dụ minh họa
Xét hàm số y = x2 - 4x + 3.
Bước 1: a = 1, b = -4, c = 3.
Bước 2: Δ = (-4)2 - 4 * 1 * 3 = 16 - 12 = 4 > 0.
Bước 3: Phương trình x2 - 4x + 3 = 0 có hai nghiệm phân biệt:
- x1 = 1
- x2 = 3
Bước 4: a = 1 > 0, parabol hướng lên.
Bước 5: Bảng xét dấu:
| x | -∞ | 1 | 3 | +∞ |
|---|---|---|---|---|
| x - 1 | - | + | + | |
| x - 3 | - | - | + | |
| y = (x-1)(x-3) | + | - | + |
Bước 6: Bảng biến thiên:
| x | -∞ | 1 | 3 | +∞ |
|---|---|---|---|---|
| y | +∞ | 0 | -1 | +∞ |
Lưu ý quan trọng
- Luôn kiểm tra kỹ các bước tính toán để tránh sai sót.
- Hiểu rõ ý nghĩa của delta và dấu của a để xác định đúng dạng của parabol.
- Sử dụng bảng xét dấu và bảng biến thiên một cách linh hoạt để phân tích hàm số.
tusach.vn hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết Bài 5 trang 94 SGK Toán 11 Tập 1 - Cánh Diều một cách hiệu quả. Chúc bạn học tốt!