Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh Diều

Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh diều

Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh Diều: Giải pháp chi tiết và dễ hiểu

Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này giúp học sinh rèn luyện kỹ năng về giới hạn của hàm số, một khái niệm nền tảng trong giải tích.

Tại tusach.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và đáp án chính xác cho Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh Diều. Mục tiêu của chúng tôi là giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc

Đề bài

Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác \(\left( {OA,OM} \right),\,\left( {OA,ON} \right),\,\left( {OA,OP} \right)\) lần lượt bằng \(\frac{\pi }{2};\,\,\frac{{7\pi }}{6};\,\, - \frac{\pi }{6}\). Chứng minh rằng tam giác MNP là tam giác đều.

Phương pháp giải - Xem chi tiết Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh diều 1

Dựa vào các giá trị lượng giác để tính từng cạnh của tam giác MNP

Lời giải chi tiết

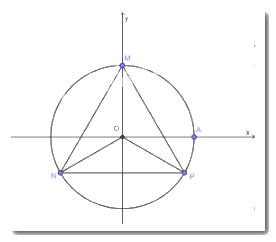
Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh diều 2

\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)

Cung MP = cung NP = cung NM

\(\Rightarrow MP = NP = NM\)

\(\Rightarrow \Delta MNP\) đều

Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn giải

Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh Diều yêu cầu học sinh tính giới hạn của hàm số tại một điểm. Để giải bài tập này, học sinh cần nắm vững định nghĩa về giới hạn của hàm số và các tính chất của giới hạn.

Nội dung bài tập:

Tính các giới hạn sau:

lim_x→2 (x² - 3x + 2) / (x - 2)
lim_x→-1 (x³ + 1) / (x + 1)
lim_x→0 (sin x) / x

Hướng dẫn giải:

Để giải các giới hạn này, chúng ta có thể sử dụng các phương pháp sau:

Phân tích thành nhân tử: Đối với các giới hạn có dạng phân số, chúng ta có thể phân tích tử và mẫu thành nhân tử để rút gọn biểu thức.
Sử dụng các công thức giới hạn đặc biệt: Ví dụ, lim_x→0 (sin x) / x = 1.
Áp dụng các tính chất của giới hạn: Ví dụ, giới hạn của một tổng bằng tổng các giới hạn, giới hạn của một tích bằng tích các giới hạn.

Giải chi tiết:

1. lim_x→2 (x² - 3x + 2) / (x - 2)

Ta phân tích tử thành nhân tử: x² - 3x + 2 = (x - 1)(x - 2)

Vậy, lim_x→2 (x² - 3x + 2) / (x - 2) = lim_x→2 (x - 1)(x - 2) / (x - 2) = lim_x→2 (x - 1) = 2 - 1 = 1

2. lim_x→-1 (x³ + 1) / (x + 1)

Ta phân tích tử thành nhân tử: x³ + 1 = (x + 1)(x² - x + 1)

Vậy, lim_x→-1 (x³ + 1) / (x + 1) = lim_x→-1 (x + 1)(x² - x + 1) / (x + 1) = lim_x→-1 (x² - x + 1) = (-1)² - (-1) + 1 = 1 + 1 + 1 = 3

3. lim_x→0 (sin x) / x

Đây là một giới hạn đặc biệt, ta có: lim_x→0 (sin x) / x = 1

Kết luận:

Vậy, đáp án của Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh Diều là:

lim_x→2 (x² - 3x + 2) / (x - 2) = 1
lim_x→-1 (x³ + 1) / (x + 1) = 3
lim_x→0 (sin x) / x = 1

Mở rộng kiến thức:

Để hiểu sâu hơn về giới hạn của hàm số, bạn có thể tham khảo thêm các tài liệu sau:

Sách giáo khoa Toán 11 tập 1 - Cánh Diều
Các bài giảng trực tuyến về giới hạn của hàm số
Các bài tập luyện tập về giới hạn của hàm số

Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh Diều. Chúc bạn học tốt!