Giải mục 2 trang 69, 70 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Giải mục 2 trang 69, 70 SGK Toán 11 tập 1 - Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 1 - Cánh Diều. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài viết này sẽ tập trung vào việc giải mục 2 trang 69 và 70, giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.
Cho hai hàm số (fleft( x right) = {x^2} - 1,gleft( x right) = x + 1.) a) Tính (mathop {lim }limits_{x to 1} fleft( x right)) và (mathop {lim }limits_{x to 1} gleft( x right).) b) Tính (mathop {lim }limits_{x to 1} left[ {fleft( x right) + gleft( x right)} right])và so sánh (mathop {lim }limits_{x to 1} fleft( x right) + mathop {lim }limits_{x to 1} gleft( x right).) c) Tính (mathop {lim }limits_{x to 1} left[ {fleft( x right) - gleft( x
Hoạt động 4
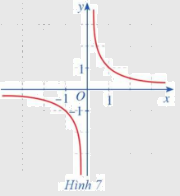
Cho hàm số \(f\left( x \right) = \frac{1}{x}\,\,\left( {x \ne 0} \right)\) có đồ thị như ở Hình 7. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới giá trị nào.
Phương pháp giải:
Quan sát đồ thị Hình 7 để trả lời câu hỏi.
Lời giải chi tiết:
a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới 0.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới 0.
Luyện tập, vận dụng 4
Tính \(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 2}}{{4x - 5}}.\)
Phương pháp giải:
- Sử dụng \(\mathop {\lim }\limits_{x \to - \infty } \frac{c}{{{x^k}}} = 0;\mathop {\lim }\limits_{x \to - \infty } c = c\)
- Sử dụng các phép toán trên giới hạn.
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 2}}{{4x - 5}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( {3 + \frac{2}{x}} \right)}}{{x\left( {4 - \frac{5}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{3 + \frac{2}{x}}}{{4 - \frac{5}{x}}} = \frac{{3 + 0}}{{4 - 0}} = \frac{3}{4}\)
Giải mục 2 trang 69, 70 SGK Toán 11 tập 1 - Cánh Diều: Hướng dẫn chi tiết và dễ hiểu
Mục 2 của chương trình Toán 11 tập 1 - Cánh Diều tập trung vào các kiến thức về phép biến hình. Đây là một phần quan trọng, đặt nền móng cho các kiến thức hình học nâng cao hơn. Việc nắm vững các khái niệm và kỹ năng giải bài tập trong mục này là rất cần thiết để đạt kết quả tốt trong môn Toán.
Nội dung chính của Mục 2
Mục 2 bao gồm các nội dung chính sau:
- Phép tịnh tiến: Định nghĩa, tính chất, và cách thực hiện phép tịnh tiến.
- Phép đối xứng trục: Định nghĩa, tính chất, và cách thực hiện phép đối xứng trục.
- Phép đối xứng tâm: Định nghĩa, tính chất, và cách thực hiện phép đối xứng tâm.
- Phép quay: Định nghĩa, tính chất, và cách thực hiện phép quay.
Giải chi tiết bài tập trang 69 SGK Toán 11 tập 1 - Cánh Diều
Trang 69 SGK Toán 11 tập 1 - Cánh Diều thường chứa các bài tập vận dụng kiến thức về phép tịnh tiến. Các bài tập này yêu cầu học sinh xác định ảnh của một điểm, một đường thẳng, hoặc một hình qua phép tịnh tiến. Để giải các bài tập này, bạn cần nắm vững định nghĩa và tính chất của phép tịnh tiến, cũng như cách biểu diễn phép tịnh tiến bằng phương trình.
Ví dụ: Bài 1 trang 69 yêu cầu tìm ảnh của điểm A(1; 2) qua phép tịnh tiến theo vectơ v = (3; -1). Giải:
Gọi A'(x'; y') là ảnh của A qua phép tịnh tiến theo vectơ v. Khi đó:
- x' = 1 + 3 = 4
- y' = 2 - 1 = 1
Vậy A'(4; 1).
Giải chi tiết bài tập trang 70 SGK Toán 11 tập 1 - Cánh Diều
Trang 70 SGK Toán 11 tập 1 - Cánh Diều thường chứa các bài tập tổng hợp về các phép biến hình. Các bài tập này yêu cầu học sinh vận dụng kiến thức về tất cả các phép biến hình đã học để giải quyết các bài toán thực tế. Để giải các bài tập này, bạn cần nắm vững định nghĩa, tính chất, và cách thực hiện của từng phép biến hình, cũng như khả năng kết hợp các phép biến hình để giải quyết bài toán.
Ví dụ: Bài 2 trang 70 yêu cầu tìm ảnh của đường thẳng d: x + y - 1 = 0 qua phép đối xứng trục Ox. Giải:
Gọi d' là ảnh của d qua phép đối xứng trục Ox. Khi đó, d' có phương trình:
x + (-y) - 1 = 0 hay x - y - 1 = 0.
Mẹo học tốt Toán 11 - Cánh Diều
- Nắm vững định nghĩa và tính chất: Đây là nền tảng để giải quyết mọi bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
- Sử dụng hình vẽ: Hình vẽ giúp bạn hình dung rõ hơn về bài toán và tìm ra lời giải.
- Tham khảo các nguồn tài liệu: Sách giáo khoa, sách bài tập, internet, và các thầy cô giáo là những nguồn tài liệu hữu ích.
Tại sao nên chọn tusach.vn để học Toán 11?
tusach.vn cung cấp:
- Lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 1 - Cánh Diều.
- Đội ngũ giáo viên giàu kinh nghiệm, nhiệt tình hỗ trợ.
- Giao diện thân thiện, dễ sử dụng.
- Cập nhật kiến thức mới nhất.
Hãy truy cập tusach.vn ngay hôm nay để học Toán 11 hiệu quả hơn!