Bài 5 trang 116 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Bài 5 trang 116 SGK Toán 11 tập 2 - Cánh Diều
Bài 5 thuộc chương trình Toán 11 tập 2, sách Cánh Diều, tập trung vào việc ôn tập về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Cho tứ diện \(OABC\) thoả mãn \(OA = a,OB = b,OC = c,\) \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {90^ \circ }\)
Đề bài
Cho tứ diện \(OABC\) thoả mãn \(OA = a,OB = b,OC = c,\) \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {90^ \circ }\). Thể tích của khối tứ diện \(OABC\) bằng:
A. \(abc\).
B. \(\frac{{abc}}{2}\).
C. \(\frac{{abc}}{3}\).
D. \(\frac{{abc}}{6}\).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).
Lời giải chi tiết
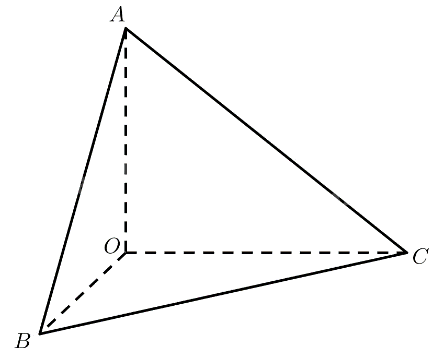
\(\left. \begin{array}{l}\widehat {AOB} = {90^ \circ } \Rightarrow OA \bot OB\\\widehat {COA} = {90^ \circ } \Rightarrow OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
\(\begin{array}{l}{S_{\Delta OBC}} = \frac{1}{2}OB.OC = \frac{1}{2}bc,h = OA = a\\ \Rightarrow {V_{OABC}} = \frac{1}{3}{S_{\Delta OBC}}.OA = \frac{1}{3}.\frac{1}{2}bc.a = \frac{{abc}}{6}\end{array}\)
Chọn D.
Bài 5 trang 116 SGK Toán 11 tập 2 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 5 trang 116 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này, được cung cấp bởi tusach.vn.
Nội dung bài tập
Bài 5 yêu cầu học sinh thực hiện các nhiệm vụ sau:
- Tính đạo hàm của các hàm số đã cho.
- Khảo sát sự biến thiên của hàm số bằng cách xác định các điểm cực trị, khoảng đồng biến, nghịch biến.
- Vẽ đồ thị hàm số.
Lời giải chi tiết
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
- Các quy tắc tính đạo hàm (quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp).
- Điều kiện để hàm số có cực trị.
- Cách xác định khoảng đồng biến, nghịch biến của hàm số.
Ví dụ: Xét hàm số y = x3 - 3x2 + 2.
- Tính đạo hàm: y' = 3x2 - 6x
- Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
- Xác định khoảng đồng biến, nghịch biến:
- Khi x < 0, y' > 0, hàm số đồng biến.
- Khi 0 < x < 2, y' < 0, hàm số nghịch biến.
- Khi x > 2, y' > 0, hàm số đồng biến.
Mẹo giải nhanh
Để giải nhanh bài tập này, học sinh có thể sử dụng các công cụ tính đạo hàm trực tuyến hoặc các phần mềm vẽ đồ thị hàm số. Tuy nhiên, việc tự giải bài tập bằng tay vẫn là cách tốt nhất để nắm vững kiến thức và rèn luyện kỹ năng.
Luyện tập thêm
Để luyện tập thêm, học sinh có thể làm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, học sinh cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi để nâng cao kiến thức và kỹ năng.
Tại sao nên chọn tusach.vn?
tusach.vn cung cấp:
- Lời giải chi tiết, dễ hiểu, được trình bày rõ ràng.
- Đáp án chính xác 100%.
- Nội dung được cập nhật thường xuyên.
- Giao diện thân thiện, dễ sử dụng.
Hãy truy cập tusach.vn ngay hôm nay để giải Bài 5 trang 116 SGK Toán 11 tập 2 - Cánh Diều và các bài tập khác một cách hiệu quả!
| Chủ đề | Nội dung |
|---|---|
| Đạo hàm | Quy tắc tính đạo hàm, ứng dụng của đạo hàm |
| Khảo sát hàm số | Tìm cực trị, khoảng đồng biến, nghịch biến |
| Đồ thị hàm số | Vẽ đồ thị hàm số dựa trên kết quả khảo sát |
| Nguồn: tusach.vn | |