Bài 6 trang 116 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Bài 6 trang 116 SGK Toán 11 tập 2 - Cánh Diều
Bài 6 thuộc chương trình Toán 11 tập 2, sách Cánh Diều, tập trung vào việc ôn tập chương 4: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các hàm số lượng giác cơ bản, tính chất của chúng và các công thức liên quan để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
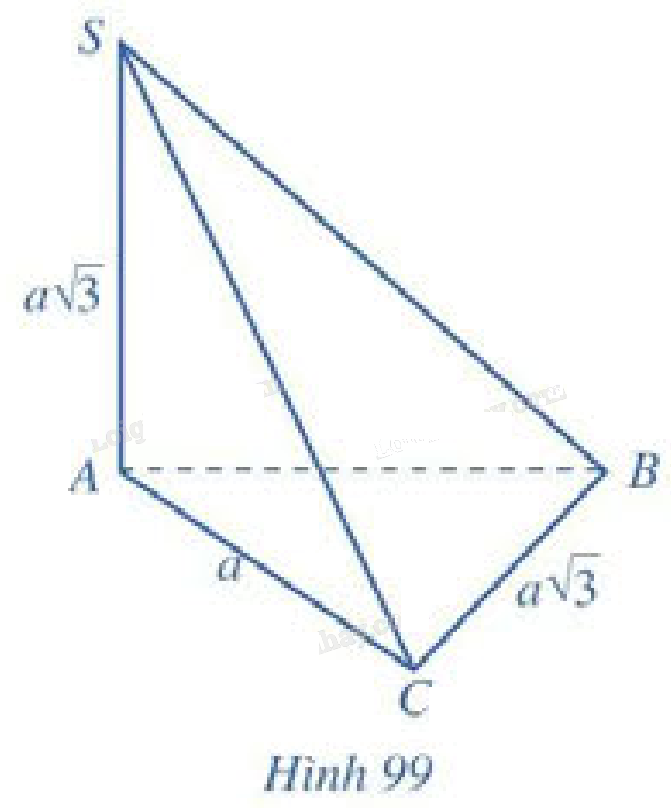
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),AC \bot BC,\)\(SA = BC = a\sqrt 3 ,AC = a\)(Hình 99).
Đề bài
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),AC \bot BC,\)\(SA = BC = a\sqrt 3 ,AC = a\)(Hình 99).
a) Tính góc giữa hai đường thẳng \(SA\) và \(BC\).
b) Tính góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABC} \right)\).
c) Tính số đo của góc nhị diện \(\left[ {B,SA,C} \right]\).
d) Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
e) Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BC\).
g) Tính thể tích của khối chóp \(S.ABC\).
Phương pháp giải - Xem chi tiết
a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).
b) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
c) Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \bot c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
d) Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
e) Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.
g) Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).
Lời giải chi tiết
a) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC \Rightarrow \left( {SA,BC} \right) = {90^ \circ }\).
b) \(SA \bot \left( {ABC} \right) \Rightarrow \left( {SC,\left( {ABC} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(\Delta SAC\) vuông tại \(A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SCA} = {60^ \circ }\)
Vậy \(\left( {SC,\left( {ABC} \right)} \right) = {60^ \circ }\).
c) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB,SA \bot AC\)
Vậy \(\widehat {BAC}\) là góc nhị diện \(\left[ {B,SA,C} \right]\).
\(\Delta ABC\) vuông tại \(C \Rightarrow \tan \widehat {BAC} = \frac{{BC}}{{AC}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {BAC} = {60^ \circ }\).
d)
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\\AC \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAC} \right)\\ \Rightarrow d\left( {B,\left( {SAC} \right)} \right) = BC = a\sqrt 3 \end{array}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC,AC \bot BC\)
\( \Rightarrow d\left( {SA,BC} \right) = AC = a\)
g) \({S_{\Delta ABC}} = \frac{1}{2}AC.BC = \frac{1}{2}a.a\sqrt 3 = \frac{{{a^2}\sqrt 3 }}{2}\)
\(\begin{array}{l}h = SA = a\sqrt 3 \\ \Rightarrow {V_{S.ABC}} = \frac{1}{3}.{S_{\Delta ABC}}.SA = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{2}.a\sqrt 3 = \frac{{{a^3}}}{2}\end{array}\)
Bài 6 trang 116 SGK Toán 11 tập 2 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 6 trang 116 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình ôn tập chương 4 về hàm số lượng giác. Bài tập này giúp học sinh củng cố kiến thức về các hàm số lượng giác, các phép biến đổi lượng giác và ứng dụng của chúng trong giải toán.
Nội dung bài tập
Bài 6 thường bao gồm các dạng bài tập sau:
- Tính giá trị của các biểu thức lượng giác: Yêu cầu tính giá trị của sin, cos, tan, cot của các góc đặc biệt hoặc các góc được cho trước.
- Giải phương trình lượng giác: Yêu cầu tìm nghiệm của các phương trình lượng giác cơ bản.
- Chứng minh đẳng thức lượng giác: Yêu cầu chứng minh các đẳng thức lượng giác bằng cách sử dụng các công thức biến đổi lượng giác.
- Ứng dụng hàm số lượng giác vào giải bài toán thực tế: Yêu cầu sử dụng kiến thức về hàm số lượng giác để giải quyết các bài toán liên quan đến hình học, vật lý hoặc các lĩnh vực khác.
Lời giải chi tiết
Dưới đây là lời giải chi tiết cho Bài 6 trang 116 SGK Toán 11 tập 2 - Cánh Diều (tùy thuộc vào nội dung cụ thể của bài tập, lời giải sẽ khác nhau). Chúng tôi sẽ trình bày lời giải cho một ví dụ minh họa:
Ví dụ: Tính giá trị của biểu thức A = sin230° + cos260°
Lời giải:
Ta có: sin30° = 1/2 và cos60° = 1/2
Do đó, A = (1/2)2 + (1/2)2 = 1/4 + 1/4 = 1/2
Hướng dẫn giải bài tập
Để giải Bài 6 trang 116 SGK Toán 11 tập 2 - Cánh Diều một cách hiệu quả, bạn nên:
- Nắm vững các công thức lượng giác cơ bản: Các công thức về sin, cos, tan, cot, các công thức cộng, trừ, nhân đôi, chia đôi góc.
- Hiểu rõ tính chất của các hàm số lượng giác: Giới trị, tính tuần hoàn, tính chẵn lẻ.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Sử dụng máy tính bỏ túi: Để kiểm tra lại kết quả và tính toán các giá trị lượng giác phức tạp.
Tài liệu tham khảo
Ngoài SGK Toán 11 tập 2 - Cánh Diều, bạn có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11: Cung cấp nhiều bài tập luyện tập khác nhau.
- Các trang web học Toán trực tuyến: tusach.vn, VietJack, Loigiaihay,...
- Các video hướng dẫn giải Toán: Trên YouTube hoặc các nền tảng video khác.
Kết luận
Bài 6 trang 116 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số lượng giác. Bằng cách nắm vững các công thức, tính chất và luyện tập thường xuyên, bạn có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. tusach.vn hy vọng rằng lời giải chi tiết và hướng dẫn trên sẽ giúp bạn học tốt môn Toán 11.
| Hàm số | Giá trị đặc biệt |
|---|---|
| sin | sin0° = 0, sin30° = 1/2, sin60° = √3/2, sin90° = 1 |
| cos | cos0° = 1, cos30° = √3/2, cos60° = 1/2, cos90° = 0 |