Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều
Bài 3 thuộc chương trình học Toán 11 tập 1, sách Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến giới hạn của hàm số. Bài tập này giúp học sinh nắm vững kiến thức về giới hạn và ứng dụng vào giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh tự tin hơn trong quá trình học tập và ôn luyện môn Toán.
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho (BI = 2IC). Chứng minh rằng IG song song với mặt phẳng (ACD).
Đề bài
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho \(BI = 2IC\). Chứng minh rằng IG song song với mặt phẳng (ACD).
Phương pháp giải - Xem chi tiết
Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với (P)
Lời giải chi tiết
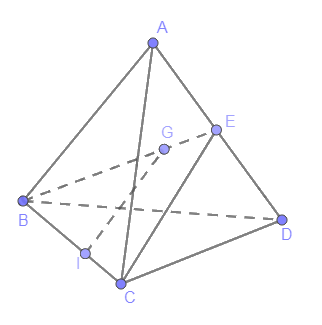
Tam giác BCE có E là trung điểm AD
Suy ra:\(\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}\)
Theo Ta lét, IG //CE
Mà CE thuộc (ACD)
Suy ra: IG // (ACD)
Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tính giới hạn của các hàm số khác nhau. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 3 yêu cầu tính các giới hạn sau:
- limx→2 (x2 - 3x + 2) / (x - 2)
- limx→-1 (x3 + 1) / (x + 1)
- limx→0 (√(x+1) - 1) / x
Lời giải chi tiết
1. Tính limx→2 (x2 - 3x + 2) / (x - 2)
Ta có thể phân tích tử thức thành nhân tử:
x2 - 3x + 2 = (x - 1)(x - 2)
Vậy, limx→2 (x2 - 3x + 2) / (x - 2) = limx→2 (x - 1)(x - 2) / (x - 2) = limx→2 (x - 1) = 2 - 1 = 1
2. Tính limx→-1 (x3 + 1) / (x + 1)
Ta có thể phân tích tử thức thành nhân tử:
x3 + 1 = (x + 1)(x2 - x + 1)
Vậy, limx→-1 (x3 + 1) / (x + 1) = limx→-1 (x + 1)(x2 - x + 1) / (x + 1) = limx→-1 (x2 - x + 1) = (-1)2 - (-1) + 1 = 1 + 1 + 1 = 3
3. Tính limx→0 (√(x+1) - 1) / x
Để tính giới hạn này, ta có thể nhân cả tử và mẫu với liên hợp của tử thức:
limx→0 (√(x+1) - 1) / x = limx→0 [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)] = limx→0 (x + 1 - 1) / [x(√(x+1) + 1)] = limx→0 x / [x(√(x+1) + 1)] = limx→0 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2
Lưu ý khi giải bài tập về giới hạn
- Luôn kiểm tra xem có thể phân tích tử thức hoặc mẫu thức thành nhân tử hay không.
- Sử dụng các công thức giới hạn cơ bản.
- Nhân cả tử và mẫu với liên hợp của tử thức hoặc mẫu thức khi cần thiết.
- Kiểm tra lại kết quả sau khi tính toán.
Ứng dụng của kiến thức về giới hạn
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học, đặc biệt là trong việc tính đạo hàm, tích phân và nghiên cứu sự hội tụ của các chuỗi. Việc nắm vững kiến thức về giới hạn là nền tảng quan trọng để học tốt các môn Toán cao cấp hơn.
Hy vọng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều và tự tin hơn trong quá trình học tập. Hãy truy cập tusach.vn để xem thêm nhiều bài giải Toán 11 khác!