Bài 1 trang 113 Toán 11 Tập 1 - Cánh Diều | Giải chi tiết & Chính xác

Bài 1 trang 113 SGK Toán 11 tập 1 - Cánh Diều

Bài 1 trang 113 SGK Toán 11 Tập 1 - Cánh Diều: Giới thiệu chung

Bài 1 trang 113 SGK Toán 11 Tập 1 - Cánh Diều là bài tập thuộc chương trình học về hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán liên quan đến việc xác định tập xác định của hàm số lượng giác và tính giá trị của hàm số tại một điểm cho trước.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Cho hình hộp ABCD.A’B’C’D’.

Đề bài

Cho hình hộp ABCD.A’B’C’D’.

a) Chứng minh rằng (ACB’) // (A’C’D’)

b) Gọi\({G_1},{G_2}\)lần lượt là giao điểm của BD’ với các mặt phẳng (ACB’) và (A’C’D’).

Chứng minh rằng\({G_1},{G_2}\)lần lượt là trọng tâm của hai tam giác ACB’ và A’C’D.

c) Chứng minh rằng \(B{G_1} = {G_1}{G_2} = D'{G_2}\)

Phương pháp giải - Xem chi tiết Bài 1 trang 113 SGK Toán 11 tập 1 - Cánh Diều 1

Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)

Lời giải chi tiết

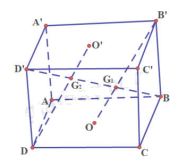
Bài 1 trang 113 SGK Toán 11 tập 1 - Cánh Diều 2

a) Ta có: AD // B’C’, AD = B’C’ nên ADC’B’ là hình bình hành

Suy ra AB’ // DC’ nên AB‘ // (A’C’D) (1)

Ta có: (ACC’A‘) là hình bình hành nên AC // A’C‘

Suy ra AC // (A’C’D‘) (2)

Mà AB‘, AC thuộc (ACB‘) (3)

Từ (1), (2), (3) suy ra (ACB‘) // (A‘C’D)

b) Gọi O, O’ lần lượt là tâm hình bình hành ABCD, A’B’C’D’

Trong (BDD’B’): B’O cắt BD’

Mà B’O thuộc (ACB’), BD’ cắt (ACB’) tại\({G_1}\)

Suy ra: B’O cắt BD’ tại\({G_1}\)

Tương tự, ta có: DO’ cắt BD’ tại\({G_2}\)

Ta có: tam giác \({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\) (do BD // B’D’)

Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)

Nên \(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{2}{3}\)

Do đó:\({G_1}\) là trọng tâm tam giác ACB’

Chứng minh tương tự ta có:\({G_2}\) là trọng tâm tam giác A’C’D

c) Ta có tam giác\({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\)

Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)

Nên \({G_1}B = \frac{1}{3}BD'(1)\)

Tương tự ta có:\(\frac{{{G_2}D'}}{{{G_2}B}} = \frac{{OD'}}{{DB}} = \frac{1}{2}\)

Nên \({G_2}D' = \frac{1}{3}{\rm{DD}}'(2)\)

Từ (1) và (2) suy ra\({G_1}B = {G_1}{G_2} = {G_2}D'\)

Bài 1 trang 113 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết

Bài 1 trang 113 SGK Toán 11 Tập 1 - Cánh Diều yêu cầu chúng ta xác định tập xác định của các hàm số sau:

a) y = √(2 - x)

Để hàm số y = √(2 - x) xác định, điều kiện là 2 - x ≥ 0. Suy ra x ≤ 2. Vậy tập xác định của hàm số là D = (-∞; 2].

b) y = 1 / (x - 3)

Để hàm số y = 1 / (x - 3) xác định, điều kiện là x - 3 ≠ 0. Suy ra x ≠ 3. Vậy tập xác định của hàm số là D = R \ {3}.

c) y = tan(x)

Hàm số y = tan(x) xác định khi cos(x) ≠ 0. Điều này tương đương với x ≠ π/2 + kπ, với k là số nguyên. Vậy tập xác định của hàm số là D = R \ {π/2 + kπ, k ∈ Z}.

d) y = cot(x)

Hàm số y = cot(x) xác định khi sin(x) ≠ 0. Điều này tương đương với x ≠ kπ, với k là số nguyên. Vậy tập xác định của hàm số là D = R \ {kπ, k ∈ Z}.

Phương pháp giải bài tập về tập xác định của hàm số

Để giải các bài tập về tập xác định của hàm số, cần nắm vững các điều kiện sau:

Với hàm số y = f(x), tập xác định là tập hợp tất cả các giá trị của x sao cho f(x) có nghĩa.
Đối với hàm căn bậc chẵn, biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0.
Đối với hàm phân thức, mẫu số phải khác 0.
Đối với hàm lượng giác, cần xem xét điều kiện xác định của từng hàm lượng giác (tan, cot).

Luyện tập thêm

Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự trong SGK Toán 11 Tập 1 - Cánh Diều và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán.

Tusach.vn - Đồng hành cùng bạn học Toán 11

Tusach.vn là website cung cấp tài liệu học tập và giải bài tập Toán 11 đầy đủ, chính xác và dễ hiểu. Chúng tôi luôn cập nhật những thông tin mới nhất và cung cấp những phương pháp giải bài tập hiệu quả nhất để giúp bạn học Toán 11 đạt kết quả tốt nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!

Bảng tóm tắt điều kiện xác định của một số hàm số thường gặp

Hàm số	Điều kiện xác định
y = √f(x)	f(x) ≥ 0
y = 1/f(x)	f(x) ≠ 0
y = tan(x)	x ≠ π/2 + kπ, k ∈ Z
y = cot(x)	x ≠ kπ, k ∈ Z