Bài 8 trang 80 Toán 11 tập 1 - Cánh Diều | Giải chi tiết & Chính xác

Bài 8 trang 80 SGK Toán 11 tập 1 - Cánh Diều

Bài 8 trang 80 SGK Toán 11 tập 1 - Cánh Diều: Giải tích

Bài 8 trang 80 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình Giải tích, tập trung vào việc ôn tập về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập Toán 11 hiệu quả.

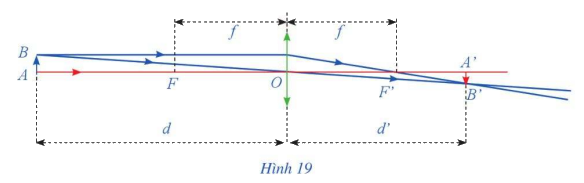
Một thấu kính hội tụ có tiêu cự là \(f\). Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ một vật thật AB và từ ảnh \(A'B'\) của nó tới quang tâm \(O\) của thấu kính như Hình 19. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\).

Đề bài

Một thấu kính hội tụ có tiêu cự là \(f\). Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ một vật thật AB và từ ảnh \(A'B'\) của nó tới quang tâm \(O\) của thấu kính như Hình 19. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\).

a) Tìm biểu thức xác định hàm số \(d' = \varphi (d)\).

b) Tìm \(\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d),\mathop {\lim }\limits_{d \to {f^ - }} \varphi (d)\) và \(\mathop {\lim }\limits_{d \to f} \varphi (d)\). Giải thích ý nghĩa của các kết quả tìm được.

Bài 8 trang 80 SGK Toán 11 tập 1 - Cánh Diều 1

Phương pháp giải - Xem chi tiết Bài 8 trang 80 SGK Toán 11 tập 1 - Cánh Diều 2

Sử dụng công thức \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\)

Lời giải chi tiết

a) Ta có \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f} \Leftrightarrow \frac{1}{{d'}} = \frac{1}{f} - \frac{1}{d} = \frac{{d - f}}{{df}} \Leftrightarrow d' = \frac{{df}}{{d - f}}\)

Ta có: \(\left\{ \begin{array}{l}df > 0\\d - f > 0,d \to {f^ + }\end{array} \right.\)

\(\begin{array}{l}\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = + \infty \end{array}\)

Ta có: \(\left\{ \begin{array}{l}df > 0\\d - f < 0,d \to {f^ - }\end{array} \right.\)

Do đó, \(\begin{array}{l}\mathop {\lim }\limits_{d \to {f^ - }} \varphi (d) = \mathop {\lim }\limits_{d \to {f^ - }} \frac{{df}}{{d - f}} = - \infty \end{array}\)

Vì \(\begin{array}{l}\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d)\ne \mathop {\lim }\limits_{d \to {f^ - }} \varphi (d)\end{array}\)

Vậy nên không tồn tại \(\begin{array}{l}\mathop {\lim }\limits_{d \to f} \varphi (d) \end{array}\)

Giải thích ý nghĩa của các kết quả tìm được: Khi khoảng cách của vật tới thấu kính mà gần với tiêu cự thì khoảng cách ảnh của vật đến thấu kính ra xa vô tận nên lúc đó bằng mắt thường mình không nhìn thấy.

Bài 8 trang 80 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn

Bài 8 trang 80 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài tập yêu cầu học sinh thực hiện các nhiệm vụ sau:

Tính đạo hàm của các hàm số cho trước.
Khảo sát sự biến thiên của hàm số bằng cách xác định các điểm cực trị, khoảng đồng biến, nghịch biến.
Vẽ đồ thị hàm số.

Lời giải chi tiết

Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:

Các quy tắc tính đạo hàm (quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp).
Điều kiện cần và đủ để hàm số đạt cực trị.
Cách xác định khoảng đồng biến, nghịch biến của hàm số.

Ví dụ: Xét hàm số y = x³ - 3x² + 2.

Tính đạo hàm: y' = 3x² - 6x.
Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 và x = 2.
Xác định khoảng đồng biến, nghịch biến:
- Khi x < 0, y' > 0, hàm số đồng biến.
- Khi 0 < x < 2, y' < 0, hàm số nghịch biến.
- Khi x > 2, y' > 0, hàm số đồng biến.
Kết luận: Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.

Mẹo giải bài tập

Để giải bài tập này một cách hiệu quả, học sinh nên:

Nắm vững các quy tắc tính đạo hàm.
Thực hành giải nhiều bài tập tương tự.
Sử dụng máy tính cầm tay để kiểm tra kết quả.

Tài liệu tham khảo

Học sinh có thể tham khảo thêm các tài liệu sau:

Sách giáo khoa Toán 11 tập 1 - Cánh Diều.
Sách bài tập Toán 11 tập 1 - Cánh Diều.
Các trang web học Toán trực tuyến.

Luyện tập thêm

Để củng cố kiến thức, học sinh có thể tự giải thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học Toán trực tuyến. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập một cách hiệu quả.

Lưu ý: Bài giải trên chỉ là một ví dụ minh họa. Học sinh cần tự giải các bài tập khác trong bài 8 trang 80 SGK Toán 11 tập 1 - Cánh Diều để hiểu rõ hơn về nội dung bài học.

Chúc các em học tốt!

STT	Bài tập	Đáp án
1	Bài 8.1	(Đáp án chi tiết tại tusach.vn)
2	Bài 8.2	(Đáp án chi tiết tại tusach.vn)