Giải mục 4 trang 102, 103 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Giải mục 4 trang 102, 103 SGK Toán 11 tập 2 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 102, 103 SGK Toán 11 tập 2 - Cánh Diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, từ đó áp dụng kiến thức vào các bài tập khác một cách hiệu quả.
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\)
Hoạt động 3
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\) song song với nhau, chiều cao của chiếc cột có đỉnh cột \(A\) là khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( P \right)\).
a) Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( P \right)\) có phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \) hay không? Vì sao?
b) Khoảng cách đó gợi nên khái niệm nào trong hình học liên quan đến đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\)?
Phương pháp giải:
Sử dụng tính chất của đường thẳng và mặt phẳng song song.
Lời giải chi tiết:
a) Trên đường thẳng \(\Delta \) lấy điểm \(B\) khác \(A\).
Kẻ \(AH \bot \left( P \right),BK \bot \left( P \right)\left( {H,K \in \left( P \right)} \right)\)
\( \Rightarrow ABKH\) là hình chữ nhật \( \Rightarrow AH = BK\)
\( \Rightarrow d\left( {A,\left( P \right)} \right) = d\left( {B,\left( P \right)} \right)\)
Vậy khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( P \right)\) không phụ thuộc vào vị trí của điểm \(A\) trên đường thẳng \(\Delta \).
b) Khoảng cách đó gợi nên khái niệm khoảng cách giữa đường thẳng và mặt phẳng song song.
Luyện tập 3
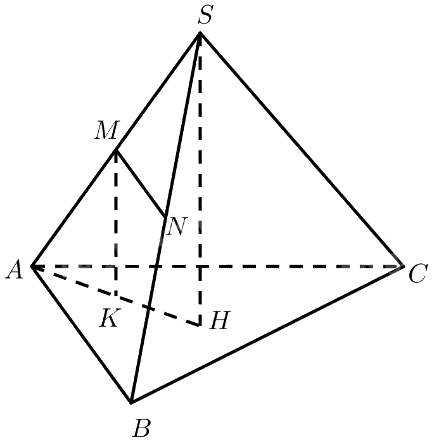
Cho hình chóp \(S.ABC\) có \(SA = a\), góc giữa \(SA\) và \(mp\left( {ABC} \right)\) là \({60^ \circ }\). Gọi \(M,N\) lần lượt là trung điểm của cạnh \(SA\) và \(SB\). Chứng minh \(MN\parallel \left( {ABC} \right)\) và tính \(d\left( {MN,\left( {ABC} \right)} \right)\).
Phương pháp giải:
‒ Cách chứng minh đường thẳng song song với mặt phẳng: Chứng minh đường thẳng đó song song với một đường thẳng nằm trên mặt phẳng.
‒ Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song: Tính khoảng cách từ một điểm trên đường thẳng đến mặt phẳng.
Lời giải chi tiết:

Ta có: \(M\) là trung điểm của \(SA\)
\(N\) là trung điểm của \(SB\)
\( \Rightarrow MN\) là đường trung bình của \(\Delta SAB\)
\(\left. \begin{array}{l} \Rightarrow MN\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {ABC} \right)\)
\( \Rightarrow d\left( {MN,\left( {ABC} \right)} \right) = d\left( {M,\left( {ABC} \right)} \right)\)
Gọi \(H\) là hình chiếu vuông góc của \(S\) lên \(\left( {ABC} \right)\)\( \Rightarrow SH \bot \left( {ABC} \right)\)
Qua \(M\) kẻ đường thẳng song song với \(SH\), cắt \(\left( {ABC} \right)\) tại \(K\)
\( \Rightarrow K \in AH,MK \bot \left( {ABC} \right) \Rightarrow d\left( {M,\left( {ABC} \right)} \right) = MK\)
\(\begin{array}{l}SH \bot \left( {ABC} \right) \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,HA} \right) = \widehat {SAH} = {60^ \circ }\\ \Rightarrow SH = SA.\sin \widehat {SAH} = \frac{{a\sqrt 3 }}{2}\end{array}\)
\(M\) là trung điểm của \(SA\), \(MK\parallel SH\)
\( \Rightarrow MK\) là đường trung bình của \(\Delta SAH\)
\( \Rightarrow MK = \frac{1}{2}AH = \frac{{a\sqrt 3 }}{4}\)
Vậy \(d\left( {MN,\left( {ABC} \right)} \right) = \frac{{a\sqrt 3 }}{4}\)
Giải mục 4 trang 102, 103 SGK Toán 11 tập 2 - Cánh Diều: Tổng quan và Phương pháp giải
Mục 4 của SGK Toán 11 tập 2 - Cánh Diều tập trung vào các kiến thức về Đường thẳng vuông góc với mặt phẳng. Đây là một phần quan trọng trong chương trình hình học không gian, đòi hỏi học sinh phải nắm vững các định nghĩa, tính chất và định lý liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trang 102, 103, đồng thời gợi ý phương pháp giải hiệu quả để các em có thể tự giải các bài tập tương tự.
Nội dung chính của Mục 4
- Định nghĩa đường thẳng vuông góc với mặt phẳng: Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
- Điều kiện để đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với một mặt phẳng khi và chỉ khi nó vuông góc với một đường thẳng nào đó nằm trong mặt phẳng đó.
- Tính chất của đường thẳng vuông góc với mặt phẳng: Đường thẳng vuông góc với mặt phẳng tạo với mặt phẳng một góc vuông.
- Ứng dụng: Giải các bài toán liên quan đến việc xác định góc giữa đường thẳng và mặt phẳng, tính khoảng cách từ một điểm đến mặt phẳng.
Giải chi tiết các bài tập trang 102, 103
Bài 1: (Trang 102)
Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SA và mặt phẳng (ABCD).
Lời giải:
- Vì SA vuông góc với mặt phẳng (ABCD) nên SA vuông góc với mọi đường thẳng nằm trong mặt phẳng (ABCD), trong đó có AB.
- Do đó, góc giữa đường thẳng SA và mặt phẳng (ABCD) chính là góc SAB.
- Xét tam giác SAB vuông tại A, ta có: tan(SAB) = SA/AB = a/a = 1.
- Suy ra, góc SAB = 45°. Vậy, góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 45°.
Bài 2: (Trang 103)
Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, BC = b, SA vuông góc với mặt phẳng (ABCD) và SA = h. Tính khoảng cách từ điểm C đến mặt phẳng (SAB).
Lời giải:
Bài toán này đòi hỏi chúng ta phải sử dụng kiến thức về khoảng cách từ một điểm đến một mặt phẳng. Để giải bài toán này, chúng ta cần:
- Tìm hình chiếu vuông góc của C lên mặt phẳng (SAB).
- Tính độ dài đoạn thẳng nối C với hình chiếu vuông góc đó.
(Lời giải chi tiết cho bài 2 sẽ được trình bày đầy đủ với các bước tính toán cụ thể, hình vẽ minh họa và các lưu ý quan trọng để giúp học sinh hiểu rõ phương pháp giải)
Mẹo và Lưu ý khi giải bài tập về Đường thẳng vuông góc với mặt phẳng
Để giải tốt các bài tập về đường thẳng vuông góc với mặt phẳng, các em cần:
- Nắm vững định nghĩa, tính chất và điều kiện của đường thẳng vuông góc với mặt phẳng.
- Sử dụng các định lý và công thức liên quan một cách linh hoạt.
- Vẽ hình minh họa để hình dung rõ bài toán.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Tusach.vn hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả này, các em sẽ tự tin hơn khi giải các bài tập về đường thẳng vuông góc với mặt phẳng trong SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt!