Giải mục 1 trang 107, 108 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Giải mục 1 trang 107, 108 SGK Toán 11 tập 2 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 107, 108 SGK Toán 11 tập 2, bộ sách Cánh Diều. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và nắm vững kiến thức trọng tâm của bài học.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Cho hình lăng trụ tam giác có các mặt bên là hình chữ nhật ở Hình 80a, 80b.
Hoạt động 1
Cho hình lăng trụ tam giác có các mặt bên là hình chữ nhật ở Hình 80a, 80b. Hãy cho biết mỗi cạnh bên của lăng trụ đó có vuông góc với các mặt đáy hay không.
Phương pháp giải:
Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
Lời giải chi tiết:
\(ABB'A'\) là hình chữ nhật \( \Rightarrow AA' \bot AB\)
\(ACC'A'\) là hình chữ nhật \( \Rightarrow AA' \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AA' \bot \left( {ABC} \right)\\AA'\parallel BB'\parallel CC'\end{array} \right\} \Rightarrow BB' \bot \left( {ABC} \right),CC' \bot \left( {ABC} \right)\)
Vậy các cạnh bên của lăng trụ đó vuông góc với các mặt đáy.
Luyện tập 1
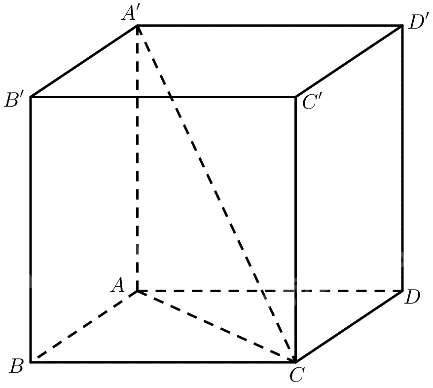
Cho hình lập phương có cạnh bằng \(a\). Tính độ dài đường chéo của hình lập phương đó.
Phương pháp giải:
Sử dụng định lí Pitago.`
Lời giải chi tiết:

\(\Delta ABC\) vuông tại \(B \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(\Delta AA'C\) vuông tại \(A \Rightarrow A'C = \sqrt {AA{'^2} + A{C^2}} = a\sqrt 3 \)
Vậy độ dài đường chéo của hình lập phương đó bằng \(a\sqrt 3 \).
Giải mục 1 trang 107, 108 SGK Toán 11 tập 2 - Cánh Diều: Tổng quan và Phương pháp giải
Mục 1 trang 107, 108 SGK Toán 11 tập 2 - Cánh Diều tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức về:
- Định nghĩa và tính chất của các hàm số lượng giác (sin, cos, tan, cot).
- Biểu diễn hình học của hàm số lượng giác.
- Phương trình lượng giác cơ bản và phương pháp giải.
- Ứng dụng của hàm số lượng giác trong việc giải quyết các bài toán thực tế.
Nội dung chi tiết các bài tập trong mục 1
Để giúp các em hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng bài tập trong mục 1 trang 107, 108 SGK Toán 11 tập 2 - Cánh Diều:
Bài 1: (Trang 107)
Bài 1 thường yêu cầu học sinh xác định tập xác định của hàm số lượng giác. Để giải bài này, các em cần nắm vững điều kiện xác định của từng hàm số lượng giác. Ví dụ:
- Hàm số y = sin(x) có tập xác định là R.
- Hàm số y = cos(x) có tập xác định là R.
- Hàm số y = tan(x) có tập xác định là R \ {kπ + π/2, k ∈ Z}.
- Hàm số y = cot(x) có tập xác định là R \ {kπ, k ∈ Z}.
Bài 2: (Trang 107)
Bài 2 thường yêu cầu học sinh xét tính chẵn, lẻ của hàm số lượng giác. Để giải bài này, các em cần nhớ:
- Hàm số chẵn là hàm số thỏa mãn f(-x) = f(x) với mọi x thuộc tập xác định.
- Hàm số lẻ là hàm số thỏa mãn f(-x) = -f(x) với mọi x thuộc tập xác định.
Ví dụ: Hàm số y = cos(x) là hàm số chẵn, hàm số y = sin(x) là hàm số lẻ.
Bài 3: (Trang 108)
Bài 3 thường yêu cầu học sinh tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác. Để giải bài này, các em có thể sử dụng các phương pháp sau:
- Sử dụng bất đẳng thức lượng giác.
- Sử dụng phương pháp đổi biến.
- Sử dụng đạo hàm (nếu đã học về đạo hàm).
Lưu ý khi giải bài tập
Khi giải các bài tập về hàm số lượng giác, các em cần lưu ý những điều sau:
- Nắm vững định nghĩa và tính chất của các hàm số lượng giác.
- Biết cách vẽ đồ thị của các hàm số lượng giác.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra lại kết quả.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 107, 108 SGK Toán 11 tập 2 - Cánh Diều. Đừng ngần ngại liên hệ với chúng tôi nếu các em có bất kỳ thắc mắc nào. Chúc các em học tốt!
| Hàm số | Tập xác định | Tính chẵn lẻ |
|---|---|---|
| y = sin(x) | R | Lẻ |
| y = cos(x) | R | Chẵn |
| y = tan(x) | R \ {kπ + π/2, k ∈ Z} | Lẻ |