Giải mục 2 trang 33, 34, 35 SGK Toán 11 tập 1 - Cánh Diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 33, 34, 35 SGK Toán 11 tập 1 - Cánh Diều. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.

Bài tập này thuộc chương trình học Toán 11 tập 1, tập trung vào các kiến thức về hàm số và đồ thị.

a) Đường thẳng (d:y = frac{1}{2}) cắt đồ thị hàm số (y = sin x,x in left[ { - pi ;pi } right]) tại hai giao điểm ({A_0},{B_0}) (Hình 34). Tìm hoành độ của hai giao điểm ({A_0},{B_0}).

HĐ 3

a) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \sin x,x \in \left[ { - \pi ;\pi } \right]\) tại hai giao điểm \({A_0},{B_0}\) (Hình 34). Tìm hoành độ của hai giao điểm \({A_0},{B_0}\).

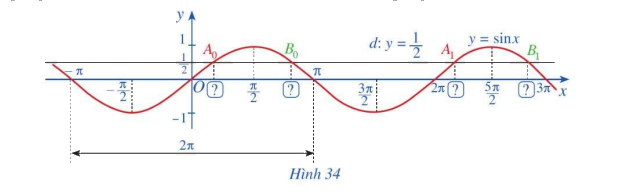
Giải mục 2 trang 33, 34, 35 SGK Toán 11 tập 1 - Cánh Diều 1

b) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \sin x,x \in \left[ {\pi ;3\pi } \right]\) tại hai giao điểm \({A_1},{B_1}\) (Hình 34). Tìm hoành độ của hai giao điểm \({A_1},{B_1}\).

Phương pháp giải:

Dựa vào kiến thức đã học về lượng giác để xác định tọa độ giao điểm

Lời giải chi tiết:

a) Hoành độ của \({A_0}\) là \(\frac{\pi }{6}\)

Hoành độ của \({B_0}\) là \(\frac{{5\pi }}{6}\)

b) Hoành độ của \({A_1}\) là \(\frac{{13\pi }}{6}\)

Hoành độ của \({B_1}\) là \(\frac{{17\pi }}{6}\)

LT - VD 3

a) Giải phương trình: \(\sin x = \frac{{\sqrt 3 }}{2}\)

b) Tìm góc lượng giác x sao cho \(\sin x = \sin {55^ \circ }\)

Phương pháp giải:

Sử dụng công thức tổng quát của phương trình sin.

Lời giải chi tiết:

a) \(\sin x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin x = \sin \frac{\pi }{3} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \pi - \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\)

\(\begin{array}{l}\sin x = \sin {55^ \circ } \Leftrightarrow \left[ \begin{array}{l}x = {55^ \circ } + k{.360^ \circ }\\x = {180^ \circ } - {55^ \circ } + k{.360^ \circ }\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = {55^ \circ } + k{.360^ \circ }\\x = {125^ \circ } + k{.360^ \circ }\end{array} \right.\\\end{array}\)

LT - VD 4

Giải phương trình \(\sin 2x = \sin \left( {x + \frac{\pi }{4}} \right)\)

Phương pháp giải:

Sử dụng công thức tổng quát của phương trình sin.

Lời giải chi tiết:

\(\sin 2x = \sin \left( {x + \frac{\pi }{4}} \right) \Leftrightarrow \left[ \begin{array}{l}2x = x + \frac{\pi }{4} + k2\pi \\2x = \pi - \left( {x + \frac{\pi }{4}} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\3x = \frac{{3\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \frac{\pi }{4} + \frac{{k2\pi }}{3}\end{array} \right.\)

Giải mục 2 trang 33, 34, 35 SGK Toán 11 tập 1 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết

Mục 2 của SGK Toán 11 tập 1 - Cánh Diều tập trung vào việc nghiên cứu sâu hơn về hàm số bậc hai, bao gồm các yếu tố như hệ số, đỉnh, trục đối xứng, và giao điểm với các trục tọa độ. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán liên quan đến hàm số bậc hai trong các chương trình học tiếp theo.

Nội dung chính của Mục 2

Hàm số bậc hai: Định nghĩa, dạng tổng quát y = ax² + bx + c (a ≠ 0).
Hệ số a: Xác định tính chất của parabol (hướng lên trên nếu a > 0, hướng xuống dưới nếu a < 0).
Đỉnh của parabol: Công thức tính tọa độ đỉnh I(x₀; y₀) với x₀ = -b/2a và y₀ = f(x₀).
Trục đối xứng của parabol: Đường thẳng x = x₀.
Giao điểm với trục hoành (Ox): Nghiệm của phương trình ax² + bx + c = 0.
Giao điểm với trục tung (Oy): Điểm có tọa độ (0; c).

Giải chi tiết các bài tập trang 33, 34, 35

Bài 1: (Trang 33)

Bài tập này yêu cầu xác định các hệ số a, b, c của hàm số bậc hai cho trước. Để giải bài tập này, các em cần nắm vững dạng tổng quát của hàm số bậc hai và so sánh với hàm số đã cho để xác định các hệ số tương ứng.

Bài 2: (Trang 34)

Bài tập này yêu cầu tìm tọa độ đỉnh của parabol. Các em cần sử dụng công thức tính tọa độ đỉnh đã học để giải bài tập này. Lưu ý kiểm tra lại các phép tính để đảm bảo tính chính xác.

Bài 3: (Trang 35)

Bài tập này yêu cầu tìm giao điểm của parabol với trục hoành. Các em cần giải phương trình bậc hai ax² + bx + c = 0 để tìm ra các nghiệm, đó chính là hoành độ giao điểm. Tung độ giao điểm sẽ là 0.

Mẹo giải bài tập hiệu quả

Nắm vững lý thuyết: Hiểu rõ các khái niệm và công thức liên quan đến hàm số bậc hai.
Phân tích đề bài: Xác định rõ yêu cầu của bài tập và các thông tin đã cho.
Sử dụng công thức chính xác: Áp dụng đúng công thức để tính toán.
Kiểm tra lại kết quả: Đảm bảo tính chính xác của các phép tính và kết quả cuối cùng.

Bảng tổng hợp các công thức quan trọng

Công thức	Mô tả
x₀ = -b/2a	Hoành độ đỉnh của parabol
y₀ = f(x₀)	Tung độ đỉnh của parabol
Δ = b² - 4ac	Biệt thức của phương trình bậc hai

Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 33, 34, 35 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt!

Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ nhé!

Giải mục 2 trang 33, 34, 35 SGK Toán 11 tập 1 - Cánh Diều

Giải mục 2 trang 33, 34, 35 SGK Toán 11 tập 1 - Cánh Diều

HĐ 3

LT - VD 3

LT - VD 4

Giải mục 2 trang 33, 34, 35 SGK Toán 11 tập 1 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết

Nội dung chính của Mục 2

Giải chi tiết các bài tập trang 33, 34, 35

Bài 1: (Trang 33)

Bài 2: (Trang 34)

Bài 3: (Trang 35)

Mẹo giải bài tập hiệu quả

Bảng tổng hợp các công thức quan trọng

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN