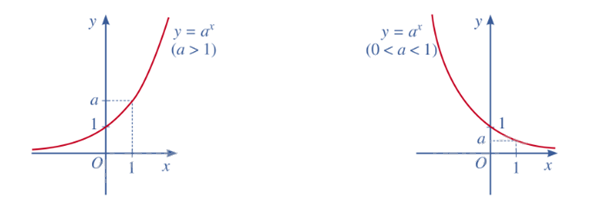Lý thuyết Hàm số mũ và Hàm số lôgarit - Nền tảng Toán 11 Cánh Diều
Hàm số mũ và hàm số lôgarit là hai khái niệm quan trọng trong chương trình Toán 11, đặc biệt trong sách Cánh Diều.
Việc nắm vững lý thuyết và các tính chất của hai hàm số này là điều kiện cần thiết để giải quyết các bài toán liên quan, đồng thời là nền tảng cho các kiến thức nâng cao hơn trong chương trình học.
1. Hàm số mũ
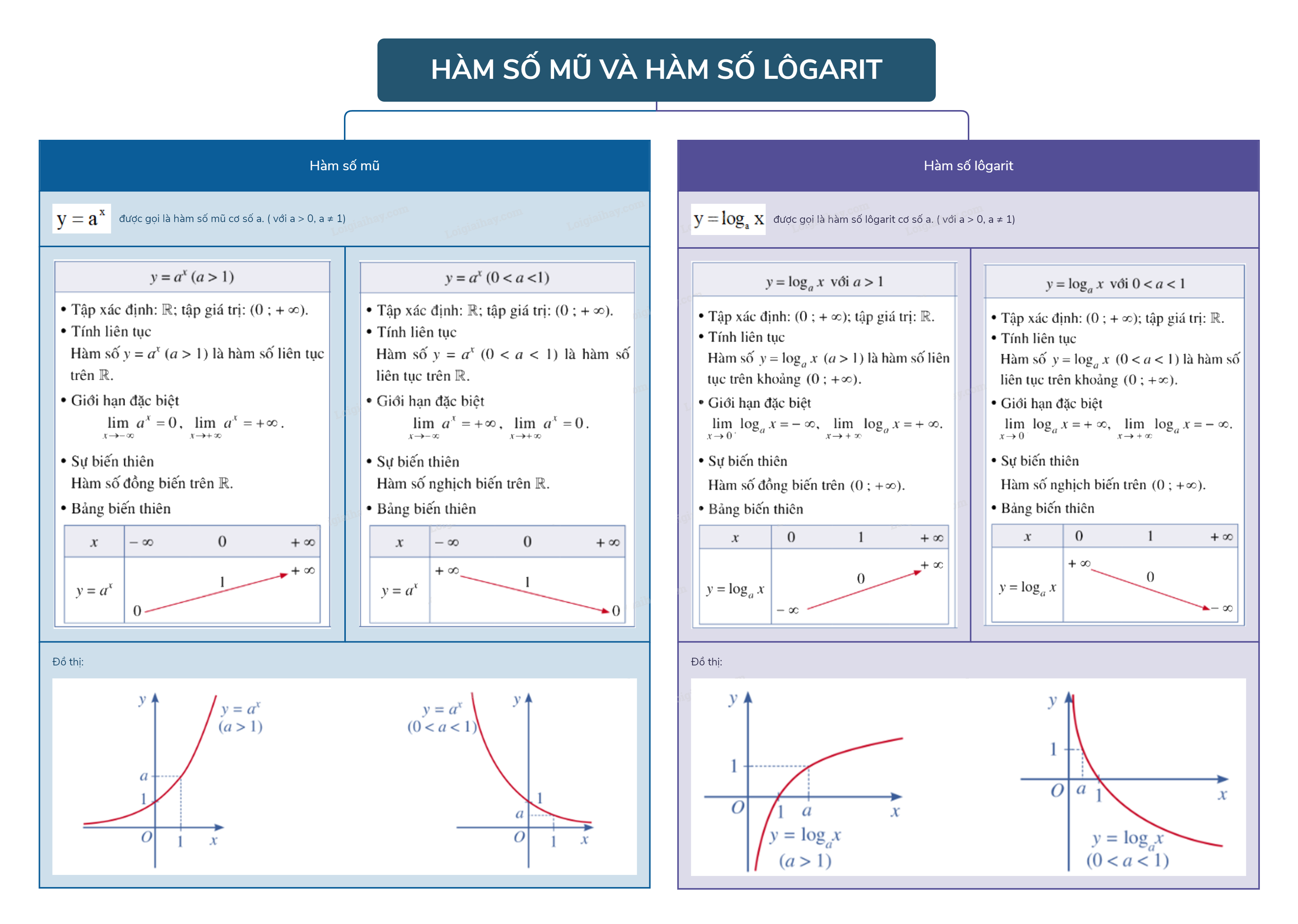
Cho số thực a ( a > 0, a \( \ne \) 1). Hàm số \(y = {a^x}\) được gọi là hàm số mũ cơ số a.
Lý Thuyết Hàm Số Mũ và Hàm Số Lôgarit - Toán 11 Cánh Diều: Tổng Quan Chi Tiết
Chào mừng các em học sinh đến với bài học lý thuyết về Hàm số mũ và Hàm số lôgarit, chương trình Toán 11 sách Cánh Diều. Bài viết này sẽ cung cấp một cái nhìn tổng quan, chi tiết và dễ hiểu về các khái niệm, tính chất, và ứng dụng của hai hàm số quan trọng này.
I. Hàm Số Mũ
1. Định nghĩa: Hàm số mũ là hàm số có dạng y = ax, trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1), và x là biến số thực.
2. Tập xác định: Tập xác định của hàm số mũ là tập số thực ℝ.
3. Tính chất:
- Hàm số mũ luôn đồng biến nếu a > 1 và nghịch biến nếu 0 < a < 1.
- Đồ thị hàm số mũ luôn đi qua điểm (0, 1).
- Hàm số mũ không có tiệm cận ngang.
4. Ví dụ:
- y = 2x là hàm số mũ đồng biến.
- y = (1/2)x là hàm số mũ nghịch biến.
II. Hàm Số Lôgarit
1. Định nghĩa: Hàm số lôgarit là hàm số nghịch đảo của hàm số mũ. Nó có dạng y = logax, trong đó a là cơ số (a > 0 và a ≠ 1), và x là biến số thực dương (x > 0).
2. Tập xác định: Tập xác định của hàm số lôgarit là tập các số thực dương (0, +∞).
3. Tính chất:
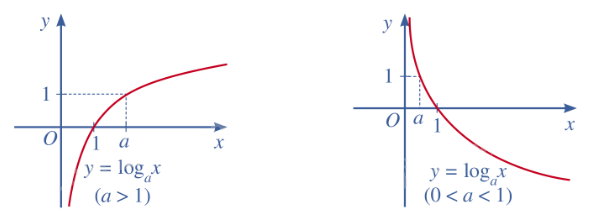
- Hàm số lôgarit đồng biến nếu a > 1 và nghịch biến nếu 0 < a < 1.
- Đồ thị hàm số lôgarit luôn đi qua điểm (1, 0).
- Hàm số lôgarit có tiệm cận đứng là đường thẳng x = 0.
4. Ví dụ:
- y = log2x là hàm số lôgarit đồng biến.
- y = log1/2x là hàm số lôgarit nghịch biến.
III. Mối Quan Hệ Giữa Hàm Số Mũ và Hàm Số Lôgarit
Hàm số mũ và hàm số lôgarit có mối quan hệ mật thiết với nhau. Cụ thể:
- alogax = x (với x > 0)
- logaax = x (với mọi x ∈ ℝ)
IV. Bài Tập Vận Dụng
Để củng cố kiến thức, các em có thể thực hành giải các bài tập sau:
- Tìm tập xác định của hàm số y = log2(x - 3).
- Vẽ đồ thị của hàm số y = 2x và y = log2x trên cùng một hệ trục tọa độ.
- Giải phương trình 2x = 8.
V. Kết Luận
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về lý thuyết Hàm số mũ và Hàm số lôgarit trong chương trình Toán 11 Cánh Diều. Việc nắm vững kiến thức này sẽ là bước đệm quan trọng cho các em trong quá trình học tập và giải quyết các bài toán phức tạp hơn. Chúc các em học tốt!