Giải mục 2 trang 75, 76 SGK Toán 11 tập 1 - Cánh Diều

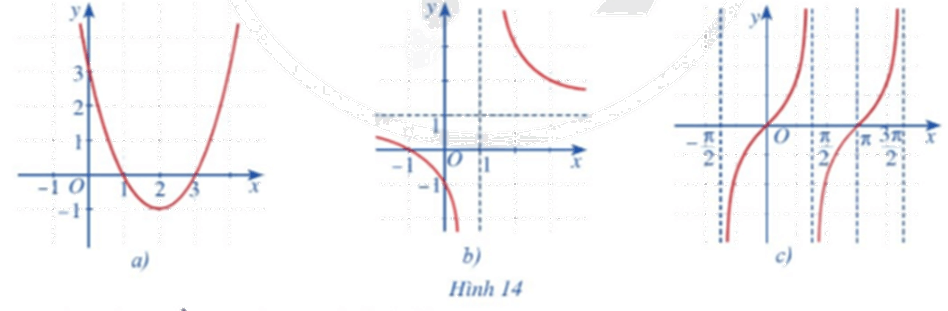
Quan sát đồ thị các hàm số: \(y = {x^2} - 4x + 3\) (Hình 14a);

\(y = \frac{{x + 1}}{{x - 1}}\,\,\left( {x \ne 1} \right)\) (Hình 14b);

\(y = \tan x\) (Hình 14c).

Và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.

Phương pháp giải:

Đồ thị hàm số liên tục trên một khoảng là “đường liền” trên khoảng đó.

Lời giải chi tiết:

Hình 14a đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ trên khoảng xác định.

Hình 14b đồ thị bị chia làm hai nhánh:

- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.

- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.

Vậy hàm số liên tục trên từng khoảng xác định.

Hình 14c đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.

Hàm số \(f\left( x \right) = \frac{{x + 2}}{{x - 8}}\) có liên tục trên mỗi khoảng \(\left( { - \infty ;8} \right),\left( {8; + \infty } \right)\) hay không?

Phương pháp giải:

Hàm phân thức hữu tỉ liên tục trên từng khoảng xác định của chúng.

Lời giải chi tiết:

Do \(f\left( x \right) = \frac{{x + 2}}{{x - 8}}\) là hàm phân thức hữu tỉ xác định khi \(x \ne 8\) nên hàm số đó liên tục trên mỗi khoảng \(\left( { - \infty ;8} \right),\left( {8; + \infty } \right)\)

Cho hai hàm số \(f\left( x \right) = {x^3} + x\) và \(g\left( x \right) = {x^2} + 1\,\,\left( {x \in \mathbb{R}} \right).\) Hãy cho biết:

a) Hai hàm số \(f\left( x \right),g\left( x \right)\) có liên tục tại \(x = 2\) hay không.

b) Các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) có liên tục tại \(x = 2\) hay không.

Phương pháp giải:

Các hàm đa thức liên tục trên \(\mathbb{R}\)

Lời giải chi tiết:

a) Ta có \(f\left( x \right),g\left( x \right)\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)

Vậy các hàm số \(f\left( x \right),g\left( x \right)\) liên tục tại \(x = 2\)

b) \(\begin{array}{l}f\left( x \right) + g\left( x \right) = {x^3} + {x^2} + x + 1\\f\left( x \right) - g\left( x \right) = {x^3} - {x^2} + x - 1\\f\left( x \right).g\left( x \right) = \left( {{x^3} + x} \right)\left( {{x^2} + 1} \right) = {x^5} + 2{x^3} + x\\\frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{{x^3} + x}}{{{x^2} + 1}} = \frac{{x\left( {{x^2} + 1} \right)}}{{{x^2} + 1}} = x\end{array}\)

Ta có \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)

Vậy các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại \(x = 2\)

Xét tính liên tục của hàm số \(f\left( x \right) = \sin x + \cos x\) trên \(\mathbb{R}.\)

Phương pháp giải:

- Hàm số lượng giác \(y = \sin x,y = \cos x\) liên tục trên \(\mathbb{R}.\)

- Định lí tính liên tục của tổng của hai hàm số liên tục:

Giả sử hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục tại điểm \({x_0}\). Khi đó các hàm số \(y = f(x) \pm g(x)\)và \(y = f(x).g(x)\) liên tục tại điểm \({x_0}\).

Lời giải chi tiết:

Vì hai làm lượng giác \(y = \sin x,y = \cos x\) liên tục trên \(\mathbb{R}\)

\( \Rightarrow f\left( x \right) = \sin x + \cos x\) liên tục trên \(\mathbb{R}\)