Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Bài 2 trang 104 SGK Toán 11 Tập 1 - Cánh Diều
Bài 2 trang 104 SGK Toán 11 Tập 1 - Cánh Diều là bài tập thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập hiệu quả.
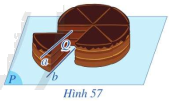
Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P)
Đề bài
Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P); mép trên và mép dưới của lát cắt lần lượt gợi nên hình ảnh hai đường thẳng a và b trong đó a song song với mặt phẳng (P). Cho biết hai đường thẳng a, b có song song với nhau hay không.
Phương pháp giải - Xem chi tiết
Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó.
Lời giải chi tiết
Hai đường thẳng a, b song song với nhau vì a song song với (P) mà (Q) cắt (P) tại giao tuyến b.
Tức là,
\(\left\{ \begin{array}{l}a \subset (Q)\\a//(P)\\(Q) \cap (P) = b\end{array} \right. \Rightarrow a//b\)
Bài 2 trang 104 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 2 trang 104 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về giới hạn của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này, được cung cấp bởi tusach.vn.
Nội dung bài tập
Bài 2 yêu cầu tính các giới hạn sau:
- limx→2 (x2 - 3x + 2) / (x - 2)
- limx→-1 (x3 + 1) / (x + 1)
- limx→0 (√(x+1) - 1) / x
Lời giải chi tiết
1. Tính limx→2 (x2 - 3x + 2) / (x - 2)
Ta có thể phân tích tử thức:
x2 - 3x + 2 = (x - 1)(x - 2)
Do đó:
limx→2 (x2 - 3x + 2) / (x - 2) = limx→2 (x - 1)(x - 2) / (x - 2) = limx→2 (x - 1) = 2 - 1 = 1
2. Tính limx→-1 (x3 + 1) / (x + 1)
Ta có thể phân tích tử thức:
x3 + 1 = (x + 1)(x2 - x + 1)
Do đó:
limx→-1 (x3 + 1) / (x + 1) = limx→-1 (x + 1)(x2 - x + 1) / (x + 1) = limx→-1 (x2 - x + 1) = (-1)2 - (-1) + 1 = 1 + 1 + 1 = 3
3. Tính limx→0 (√(x+1) - 1) / x
Để tính giới hạn này, ta sử dụng phương pháp nhân liên hợp:
limx→0 (√(x+1) - 1) / x = limx→0 [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)] = limx→0 (x + 1 - 1) / [x(√(x+1) + 1)] = limx→0 x / [x(√(x+1) + 1)] = limx→0 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2
Kết luận
Vậy, kết quả của các giới hạn là:
- limx→2 (x2 - 3x + 2) / (x - 2) = 1
- limx→-1 (x3 + 1) / (x + 1) = 3
- limx→0 (√(x+1) - 1) / x = 1/2
Mẹo giải nhanh
Khi gặp các bài toán tính giới hạn, hãy chú ý đến các phương pháp sau:
- Phân tích tử thức và mẫu thức để rút gọn biểu thức.
- Sử dụng các công thức giới hạn cơ bản.
- Áp dụng phương pháp nhân liên hợp để khử dạng vô định.
Hy vọng lời giải chi tiết này sẽ giúp các bạn hiểu rõ hơn về Bài 2 trang 104 SGK Toán 11 Tập 1 - Cánh Diều. Hãy truy cập tusach.vn để xem thêm nhiều bài giải Toán 11 khác!