Bài 4 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Bài 4 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Bài 4 thuộc chương trình Toán 11 tập 2, sách Cánh Diều, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các hàm số lượng giác cơ bản, tính chất của chúng và các công thức liên quan để giải quyết các bài toán cụ thể.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
Đề bài
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(C{\rm{D}}\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\).
c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
Phương pháp giải - Xem chi tiết
‒ Cách tính khoảng cách từ một điểm đến một đường thẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên đường thẳng.
‒ Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
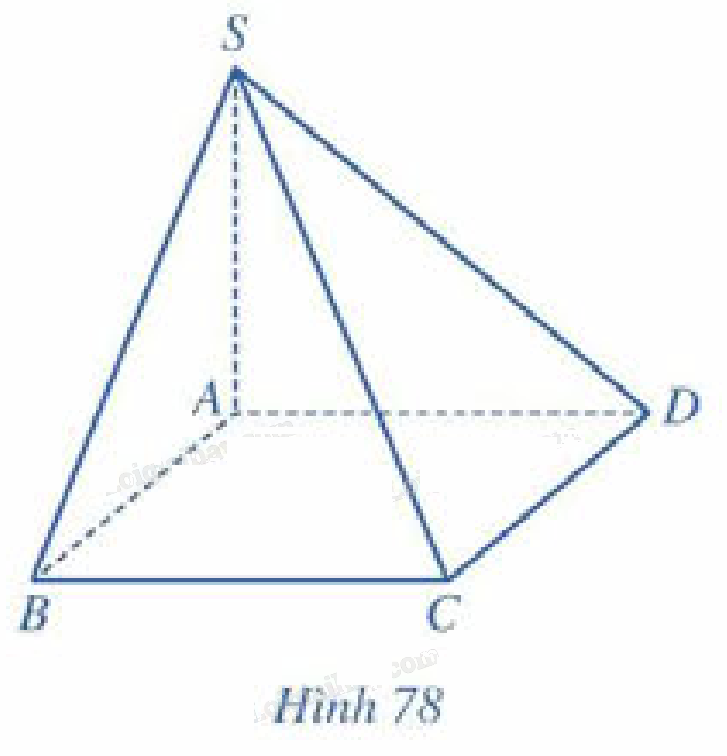
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).
Giải Bài 4 trang 106 SGK Toán 11 tập 2 - Cánh Diều: Ôn tập chương 3 - Hàm số lượng giác
Bài 4 trang 106 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong quá trình ôn tập chương 3 về hàm số lượng giác. Bài tập này giúp học sinh củng cố kiến thức đã học, rèn luyện kỹ năng giải toán và chuẩn bị cho các bài kiểm tra, thi cử sắp tới. Dưới đây là lời giải chi tiết và cách làm bài tập này, được cung cấp bởi Tusach.vn.
Nội dung bài tập:
Bài 4 yêu cầu học sinh thực hiện các nhiệm vụ sau:
- Xác định tập xác định của hàm số lượng giác.
- Tìm tập giá trị của hàm số lượng giác.
- Xác định tính đơn điệu của hàm số lượng giác.
- Giải các phương trình lượng giác cơ bản.
- Vận dụng các kiến thức về hàm số lượng giác để giải quyết các bài toán thực tế.
Lời giải chi tiết:
Để giải bài 4 trang 106 SGK Toán 11 tập 2 - Cánh Diều, học sinh cần nắm vững các kiến thức sau:
- Định nghĩa các hàm số lượng giác: sin, cos, tan, cot và các tính chất của chúng.
- Tập xác định và tập giá trị của các hàm số lượng giác.
- Tính đơn điệu của các hàm số lượng giác trên các khoảng xác định.
- Các công thức lượng giác cơ bản: công thức cộng, trừ, nhân đôi, chia đôi.
- Phương pháp giải phương trình lượng giác: biến đổi phương trình về dạng cơ bản, sử dụng các công thức lượng giác để giải.
Ví dụ minh họa:
Giả sử bài tập yêu cầu tìm tập xác định của hàm số y = tan(2x). Để giải bài tập này, học sinh cần nhớ rằng hàm số tan(x) có tập xác định là tập hợp tất cả các số thực trừ các số có dạng (π/2) + kπ, với k là số nguyên. Do đó, tập xác định của hàm số y = tan(2x) là tập hợp tất cả các số thực x sao cho 2x ≠ (π/2) + kπ, tức là x ≠ (π/4) + (kπ/2), với k là số nguyên.
Mẹo giải nhanh:
Để giải nhanh các bài tập về hàm số lượng giác, học sinh nên:
- Nắm vững các định nghĩa, tính chất và công thức lượng giác cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
- Kiểm tra lại kết quả sau khi giải xong bài tập.
Tầm quan trọng của việc ôn tập:
Việc ôn tập chương 3 về hàm số lượng giác là rất quan trọng vì:
- Hàm số lượng giác là một trong những chủ đề quan trọng trong chương trình Toán 11.
- Kiến thức về hàm số lượng giác được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, kỹ thuật, kinh tế.
- Việc nắm vững kiến thức về hàm số lượng giác sẽ giúp học sinh giải quyết các bài toán phức tạp hơn trong các chương trình học tiếp theo.
Tusach.vn hy vọng rằng lời giải chi tiết và cách làm bài 4 trang 106 SGK Toán 11 tập 2 - Cánh Diều này sẽ giúp học sinh hiểu rõ hơn về hàm số lượng giác và rèn luyện kỹ năng giải toán hiệu quả. Chúc các em học tập tốt!
| Hàm số | Tập xác định | Tập giá trị |
|---|---|---|
| y = sin(x) | R | [-1, 1] |
| y = cos(x) | R | [-1, 1] |
| y = tan(x) | R \ {π/2 + kπ} | R |