Lý thuyết Đạo hàm cấp hai - Toán 11 Cánh diều
Tổng quan nội dung
Lý thuyết Đạo hàm cấp hai - Toán 11 Cánh diều
Chào mừng bạn đến với bài học về Lý thuyết Đạo hàm cấp hai trong chương trình Toán 11 Cánh diều. Bài viết này sẽ cung cấp kiến thức nền tảng, công thức quan trọng và các ví dụ minh họa để bạn hiểu rõ về đạo hàm cấp hai và ứng dụng của nó trong việc giải quyết các bài toán thực tế.
Đạo hàm cấp hai là một khái niệm quan trọng trong giải tích, giúp chúng ta hiểu rõ hơn về sự thay đổi của tốc độ thay đổi của một hàm số.
1. Định nghĩa
1. Định nghĩa
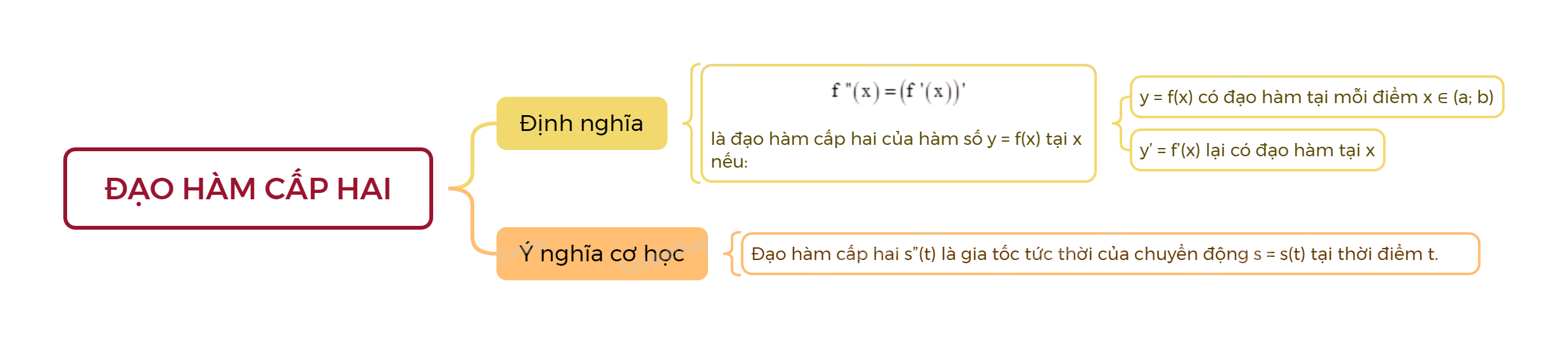
Giả sử hàm số y = f(x) có đạo hàm y’ = f’(x) tại mọi điểm \(x \in \left( {a;b} \right)\). Nếu hàm số y’ = f’(x) tiếp tục có đạo hàm tại x thì ta gọi đạo hàm của y’ tại x là đạo hàm cấp hai của hàm số y = f(x) tại x, kí hiệu là y” hoặc f”(x).
2. Ý nghĩa cơ học
Đạo hàm cấp hai s”(t) là gia tốc tức thời của chuyển động s = s(t) tại thời điểm t.
Lý Thuyết Đạo Hàm Cấp Hai - Toán 11 Cánh Diều: Giải Thích Chi Tiết và Bài Tập Áp Dụng
Chào mừng các em học sinh đến với bài học về Lý thuyết Đạo hàm cấp hai trong chương trình Toán 11 Cánh Diều. Đây là một phần kiến thức quan trọng, giúp các em hiểu sâu hơn về sự biến thiên của hàm số và ứng dụng trong nhiều lĩnh vực khác nhau.
1. Đạo Hàm Cấp Hai Là Gì?
Trước khi đi vào lý thuyết, chúng ta cần ôn lại khái niệm về đạo hàm cấp một. Đạo hàm cấp một của một hàm số f(x) tại một điểm x, ký hiệu là f'(x), biểu thị tốc độ thay đổi tức thời của hàm số tại điểm đó. Đạo hàm cấp hai, ký hiệu là f''(x), là đạo hàm của đạo hàm cấp một. Nói cách khác, đạo hàm cấp hai biểu thị tốc độ thay đổi của tốc độ thay đổi của hàm số.
2. Công Thức Tính Đạo Hàm Cấp Hai
Để tính đạo hàm cấp hai, chúng ta thực hiện hai bước:
- Tính đạo hàm cấp một f'(x).
- Tính đạo hàm của f'(x) để được đạo hàm cấp hai f''(x).
Một số công thức đạo hàm cơ bản cần nhớ:
- (xn)' = nxn-1
- (sin x)' = cos x
- (cos x)' = -sin x
- (ex)' = ex
- (ln x)' = 1/x
3. Ví Dụ Minh Họa
Ví dụ 1: Tính đạo hàm cấp hai của hàm số f(x) = x3 + 2x2 - 5x + 1
Giải:
- f'(x) = 3x2 + 4x - 5
- f''(x) = 6x + 4
Ví dụ 2: Tính đạo hàm cấp hai của hàm số f(x) = sin(2x)
Giải:
- f'(x) = 2cos(2x)
- f''(x) = -4sin(2x)
4. Ứng Dụng Của Đạo Hàm Cấp Hai
Đạo hàm cấp hai có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác:
- Xác định tính lồi, lõm của hàm số: Nếu f''(x) > 0 trên một khoảng, hàm số f(x) lồi trên khoảng đó. Nếu f''(x) < 0 trên một khoảng, hàm số f(x) lõm trên khoảng đó.
- Tìm điểm uốn: Điểm uốn là điểm mà tại đó hàm số thay đổi từ lồi sang lõm hoặc ngược lại.
- Giải các bài toán vật lý: Đạo hàm cấp hai được sử dụng để mô tả gia tốc trong chuyển động.
5. Bài Tập Áp Dụng
Hãy tự luyện tập với các bài tập sau để củng cố kiến thức:
- Tính đạo hàm cấp hai của hàm số f(x) = 4x4 - 3x2 + 7
- Tính đạo hàm cấp hai của hàm số f(x) = cos(3x)
- Xác định khoảng hàm số f(x) = x3 - 6x2 + 9x + 1 lồi và lõm.
6. Lời Khuyên Khi Học Lý Thuyết Đạo Hàm Cấp Hai
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Hiểu rõ ứng dụng của đạo hàm cấp hai trong thực tế.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về Lý thuyết Đạo hàm cấp hai - Toán 11 Cánh Diều. Chúc các em học tập tốt!