Bài 3 trang 31 SGK Toán 11 tập 1 - Cánh diều
Tổng quan nội dung
Bài 3 trang 31 SGK Toán 11 Tập 1 - Cánh Diều: Giải pháp tối ưu
Bài 3 trang 31 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
Đề bài
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
a) y = sinx trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
b) y = cosx trên khoảng \(\left( { - 20\pi ; - 19\pi } \right),\left( { - 9\pi ; - 8\pi } \right)\)
Phương pháp giải - Xem chi tiết
Sử dụng khoản biến thiên của hàm số sin x, cos x.
Lời giải chi tiết
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
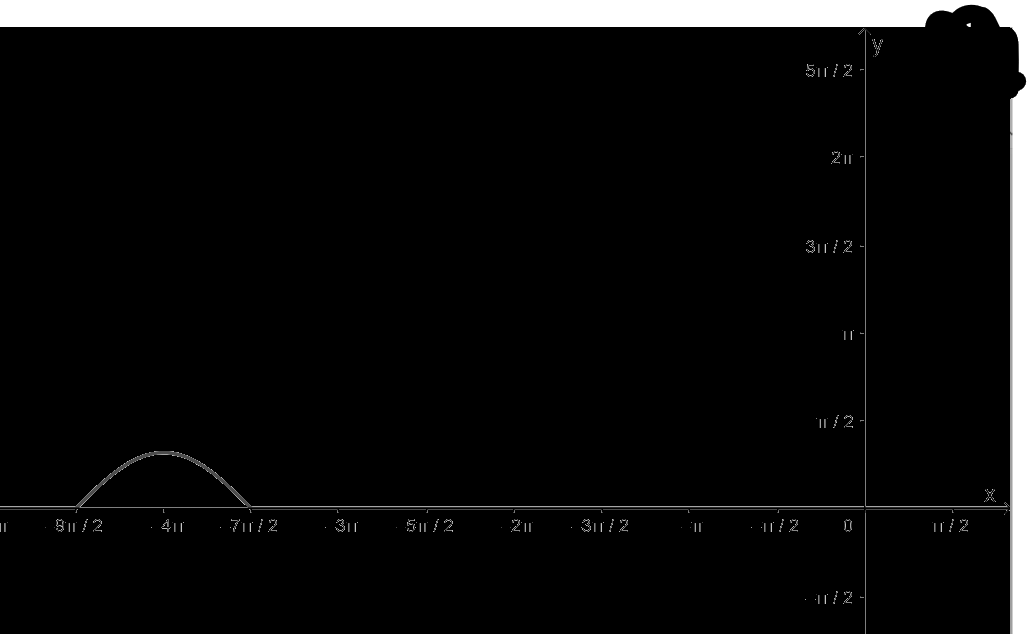
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
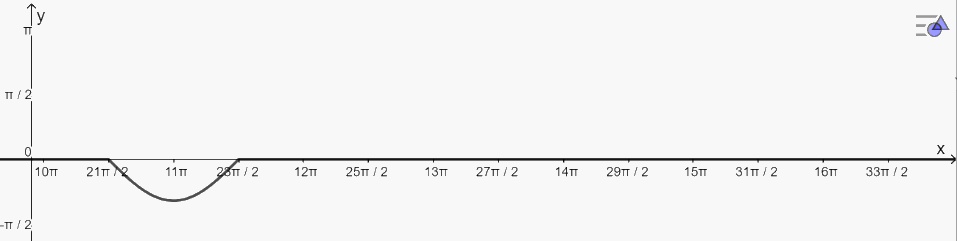
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
b) Xét hàm số \(y = \cos x\):
Do \(\left( { - 20\pi ; - 19\pi } \right) = \left( {0 - 20\pi ;\pi - 20\pi } \right)\)nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 20\pi ; - 19\pi } \right)\)
Do \(\left( { - 9\pi ; - 8\pi } \right) = \left( { - \pi - 8\pi ;0 - 8\pi } \right)\) nên hàm số \(y = \cos x\) đồng biến trên khoảng \(\left( { - 9\pi ; - 8\pi } \right)\)
Bài 3 trang 31 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 3 trang 31 SGK Toán 11 Tập 1 - Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng tính giới hạn của hàm số. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và định lý liên quan đến giới hạn, đặc biệt là giới hạn của hàm số tại một điểm và giới hạn vô cùng.
Nội dung bài tập
Bài 3 thường yêu cầu học sinh tính giới hạn của các hàm số đơn giản, hoặc các hàm số phức tạp hơn được xây dựng từ các hàm số cơ bản. Các dạng bài tập thường gặp bao gồm:
- Tính giới hạn của hàm số đa thức.
- Tính giới hạn của hàm số hữu tỉ.
- Tính giới hạn của hàm số chứa căn thức.
- Sử dụng các định lý về giới hạn để đơn giản hóa biểu thức và tính giới hạn.
Lời giải chi tiết
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích lời giải chi tiết cho từng phần của bài tập.
Ví dụ: Giả sử bài tập yêu cầu tính limx→2 (x2 - 4) / (x - 2)
- Phân tích: Hàm số có dạng (x2 - 4) / (x - 2). Khi x = 2, mẫu số bằng 0, do đó chúng ta cần đơn giản hóa biểu thức trước khi tính giới hạn.
- Đơn giản hóa: Ta có thể phân tích tử số thành (x - 2)(x + 2). Vậy biểu thức trở thành (x - 2)(x + 2) / (x - 2).
- Rút gọn: Khi x ≠ 2, ta có thể rút gọn biểu thức thành x + 2.
- Tính giới hạn:limx→2 (x + 2) = 2 + 2 = 4.
Vậy, limx→2 (x2 - 4) / (x - 2) = 4.
Mẹo giải nhanh
Để giải nhanh các bài tập về giới hạn, học sinh có thể áp dụng một số mẹo sau:
- Sử dụng các định lý về giới hạn để đơn giản hóa biểu thức.
- Phân tích tử số và mẫu số thành nhân tử để rút gọn biểu thức.
- Sử dụng quy tắc L'Hôpital khi gặp các dạng giới hạn vô định.
Bài tập tương tự
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh có thể tự giải các bài tập tương tự sau:
- Tính limx→1 (x2 - 1) / (x - 1).
- Tính limx→0 (sin x) / x.
- Tính limx→∞ (1 + 1/x)x.
Kết luận
Bài 3 trang 31 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính giới hạn của hàm số. Bằng cách nắm vững các khái niệm và định lý liên quan, cùng với việc áp dụng các mẹo giải nhanh, học sinh có thể giải quyết bài tập này một cách hiệu quả và đạt kết quả tốt trong môn Toán 11.
tusach.vn hy vọng rằng lời giải chi tiết và hướng dẫn trên sẽ giúp ích cho các em trong quá trình học tập. Chúc các em học tốt!