Bài 10 trang 21 SGK Toán 11 Tập 1 - Cánh Diều: Giải tích hàm số
Bài 10 thuộc chương trình giải tích hàm số lớp 11, tập trung vào việc xét tính đơn điệu của hàm số. Bài tập yêu cầu học sinh vận dụng các kiến thức về đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập Toán 11 hiệu quả.
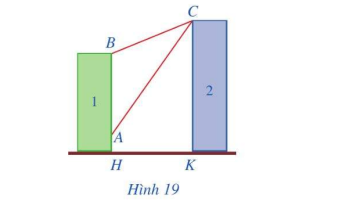
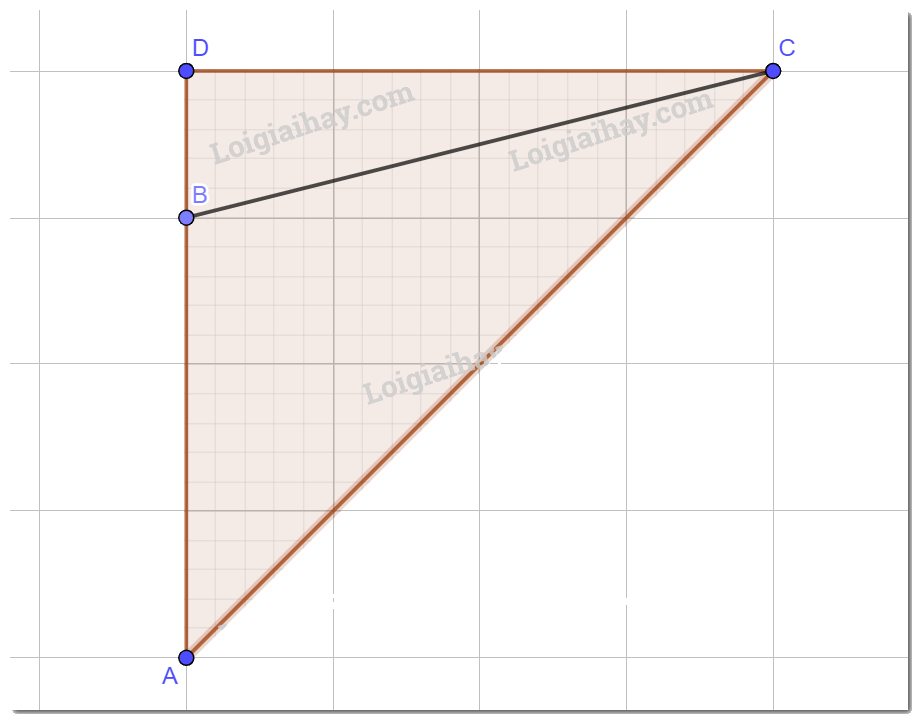
Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là (HK = 20m). Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C.
Bài 10 trang 21 SGK Toán 11 Tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 10 trang 21 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về xét tính đơn điệu của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài tập yêu cầu xét tính đơn điệu của các hàm số sau:
- f(x) = 2x3 - 3x2 + 1
- g(x) = x4 - 4x3 + 4x2 + 1
Lời giải chi tiết
a) Xét hàm số f(x) = 2x3 - 3x2 + 1
Bước 1: Tính đạo hàm f'(x)
f'(x) = 6x2 - 6x = 6x(x - 1)
Bước 2: Tìm các điểm dừng của hàm số
f'(x) = 0 ⇔ 6x(x - 1) = 0 ⇔ x = 0 hoặc x = 1
Bước 3: Lập bảng xét dấu f'(x)
| x | -∞ | 0 | 1 | +∞ |
|---|
| f'(x) | + | - | + |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Kết luận:
- Hàm số f(x) đồng biến trên các khoảng (-∞; 0) và (1; +∞)
- Hàm số f(x) nghịch biến trên khoảng (0; 1)
b) Xét hàm số g(x) = x4 - 4x3 + 4x2 + 1
Bước 1: Tính đạo hàm g'(x)
g'(x) = 4x3 - 12x2 + 8x = 4x(x2 - 3x + 2) = 4x(x - 1)(x - 2)
Bước 2: Tìm các điểm dừng của hàm số
g'(x) = 0 ⇔ 4x(x - 1)(x - 2) = 0 ⇔ x = 0, x = 1, x = 2
Bước 3: Lập bảng xét dấu g'(x)
| x | -∞ | 0 | 1 | 2 | +∞ |
|---|
| g'(x) | - | + | - | + |
| g(x) | Nghịch biến | Đồng biến | Nghịch biến | Đồng biến |
Kết luận:
- Hàm số g(x) nghịch biến trên các khoảng (-∞; 0) và (1; 2)
- Hàm số g(x) đồng biến trên các khoảng (0; 1) và (2; +∞)
Lưu ý khi giải bài tập
- Luôn tính đạo hàm chính xác.
- Xác định đúng các điểm dừng của hàm số.
- Lập bảng xét dấu đạo hàm một cách cẩn thận để xác định khoảng đồng biến, nghịch biến.
Hy vọng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về cách giải Bài 10 trang 21 SGK Toán 11 Tập 1 - Cánh Diều. Hãy luyện tập thêm nhiều bài tập tương tự để nắm vững kiến thức và kỹ năng giải bài tập Toán 11.