Lý thuyết Phép tính lũy thừa với số mũ thực - Toán 11 Cánh diều
Tổng quan nội dung
Lý thuyết Phép tính lũy thừa với số mũ thực - Toán 11 Cánh diều
Bài viết này cung cấp đầy đủ và chi tiết lý thuyết về phép tính lũy thừa với số mũ thực, thuộc chương trình Toán 11 sách Cánh diều.
Chúng ta sẽ cùng nhau khám phá các định nghĩa, tính chất, công thức quan trọng và các ví dụ minh họa để bạn có thể hiểu rõ và áp dụng kiến thức vào giải bài tập một cách hiệu quả.
1. Phép tính lũy thừa với số mũ nguyên
1. Phép tính lũy thừa với số mũ nguyên
Cho số thực a khác 0 và số nguyên dương n. Ta đặt \({a^{ - n}} = \frac{1}{{{a^n}}}\).
Chú ý:
- \({0^0}\) và \({0^{ - n}}\) (n nguyên dương) không có nghĩa.
- Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.
2. Căn bậc n
a) Định nghĩa
Cho số thực a và số nguyên dương n (n \( \ge \) 2). Số b được gọi là căn bậc n của số a nếu \({b^n} = a\).
Nhận xét:
- Với n lẻ và a \( \in \mathbb{R}\): Có duy nhất một căn bậc n của a, kí hiệu là \(\sqrt[n]{a}\).
- Với n chẵn, ta xét ba trường hợp sau:
+) a < 0: Không tồn tại căn bậc n của a.
+) a = 0: Có một căn bậc n của a là số 0.
+) a > 0: Có hai căn bậc n của a là hai số đối nhau, giá trị dương kí hiệu là \(\sqrt[n]{a}\), còn giá trị âm kí hiệu là \( - \sqrt[n]{a}\).
b) Tính chất
- \(\sqrt[n]{{{a^n}}} = \left\{ \begin{array}{l}a\,nếu\,n\,lẻ\\\left| a \right|\,nếu\,n\,chẵn\end{array} \right.\)
- \(\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}\)
- \(\frac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}} = \sqrt[n]{{\frac{a}{b}}}\)
- \({\left( {\sqrt[n]{a}} \right)^m} = \sqrt[n]{{{a^m}}}\)
- \(\sqrt[n]{{\sqrt[k]{a}}} = \sqrt[{nk}]{a}\)
(Ở mỗi công thức trên, ta giả sử các biểu thức xuất hiện trong đó là có nghĩa).
3. Phép tính lũy thừa với số mũ hữu tỉ
Cho số thực a dương và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m \in \mathbb{Z},n \in \mathbb{N},n \ge 2\). Lũy thừa của a với số mũ r xác định bởi: \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
Nhận xét:
- \({a^{\frac{1}{n}}} = \sqrt[n]{a}\left( {a > 0,n \in \mathbb{N},n \ge 2} \right)\).
- Lũy thừa với số mũ hữu tỉ của số thực dương có đầy đủ các tính chất của lũy thừa với số mũ nguyên.
4. Phép tính lũy thừa với số mũ thực
a) Định nghĩa
Cho a là số thực dương, \(\alpha \) là số vô tỉ, \(\left( {{r_n}} \right)\) là dãy số hữu tỉ và \(\lim {r_n} = \alpha \). Giới hạn của dãy số \(\left( {{a^{{r_n}}}} \right)\) gọi là lũy thừa của a với số mũ \(\alpha \), kí hiệu \({a^\alpha }\), \({a^\alpha } = \lim {a^{{r_n}}}\).
b) Tính chất
- Cho a, b là những số thực dương; \(\alpha ,\beta \) là những số thực tùy ý. Khi đó, ta có:
\({a^\alpha }.{a^\beta } = {a^{\alpha + \beta }}\); \({\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha }\); \({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\); \(\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha - \beta }}\); \({\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha \beta }}\).
- Nếu a > 1 thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha > \beta \).
Nếu 0 < a < 1 thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha < \beta \).
- Cho 0 < a < b, \(\alpha \) là một số thực. Ta có:
\({a^\alpha } < {b^\alpha } \Leftrightarrow \alpha > 0\); \({a^\alpha } > {b^\alpha } \Leftrightarrow \alpha < 0\).
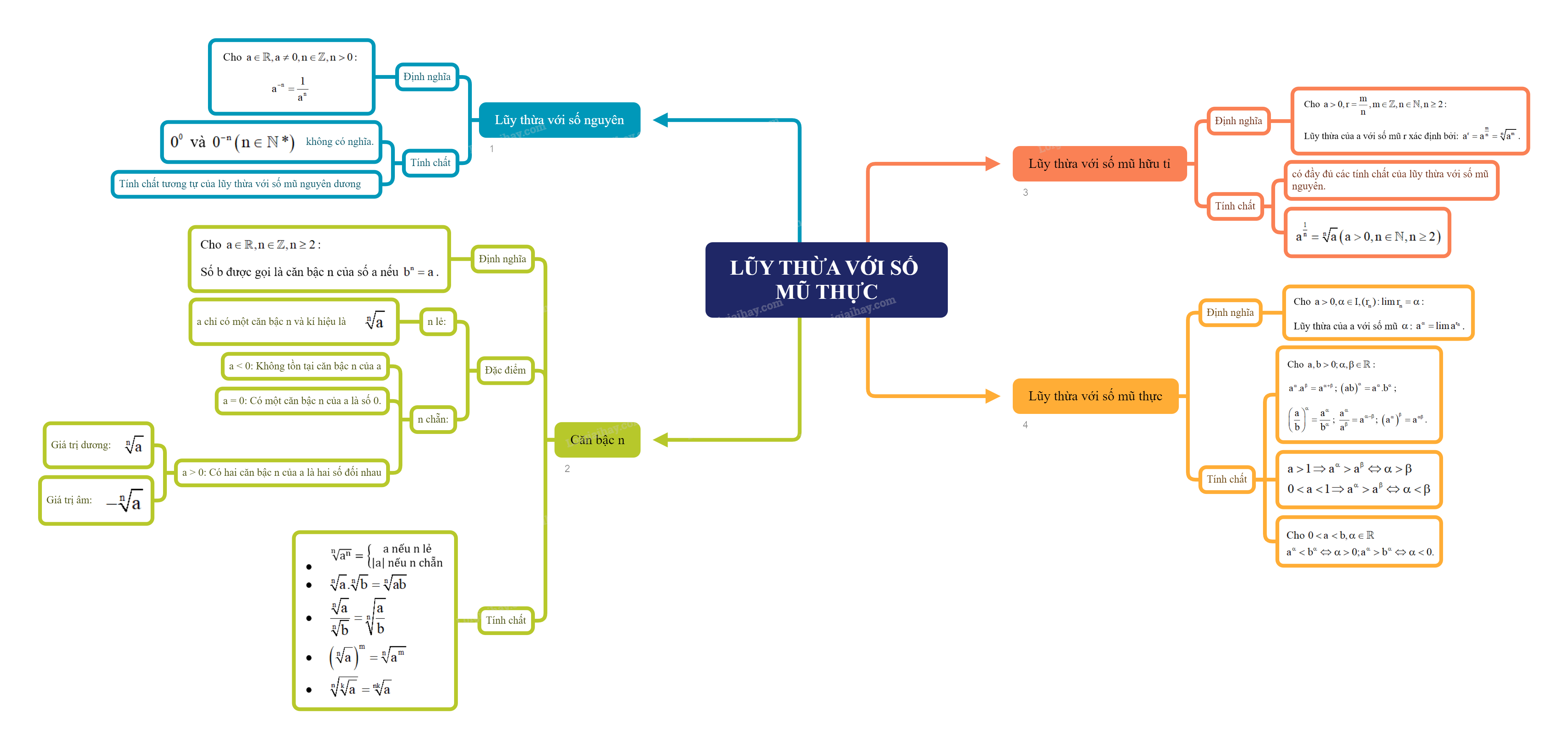
Lý Thuyết Phép Tính Lũy Thừa Với Số Mũ Thực - Toán 11 Cánh Diều: Tổng Quan Chi Tiết
Phép tính lũy thừa với số mũ thực là một phần quan trọng trong chương trình Toán 11, đặc biệt là trong sách giáo khoa Cánh Diều. Nó mở rộng khái niệm lũy thừa từ số mũ nguyên sang số mũ thực, tạo nền tảng cho việc học các khái niệm toán học nâng cao hơn như hàm số mũ và logarit.
1. Định Nghĩa Lũy Thừa Với Số Mũ Thực
Với a > 0 và α là một số thực, lũy thừa của a với số mũ α, ký hiệu là aα, là một số thực duy nhất được xác định bởi:
- Nếu α là số nguyên dương, aα = a × a × ... × a (α lần)
- Nếu α = 0, a0 = 1
- Nếu α là số nguyên âm, aα = 1 / a-α
- Nếu α là số hữu tỉ, α = m/n (m, n là số nguyên, n > 0), aα = n√am
- Nếu α là số vô tỉ, aα được định nghĩa thông qua giới hạn của các lũy thừa với số mũ hữu tỉ tiến tới α.
2. Tính Chất Của Lũy Thừa Với Số Mũ Thực
Các tính chất sau đây đóng vai trò quan trọng trong việc đơn giản hóa và giải quyết các bài toán liên quan đến lũy thừa với số mũ thực:
- ax . ay = ax+y
- ax / ay = ax-y
- (ax)y = axy
- (a . b)x = ax . bx
- (a / b)x = ax / bx
3. Ví Dụ Minh Họa
Ví dụ 1: Tính 82/3
Giải: 82/3 = (81/3)2 = 22 = 4
Ví dụ 2: Rút gọn biểu thức: (23 . 53)2
Giải: (23 . 53)2 = (2 . 5)3.2 = 106 = 1,000,000
4. Ứng Dụng Của Lũy Thừa Với Số Mũ Thực
Lũy thừa với số mũ thực có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
- Khoa học tự nhiên: Mô tả sự tăng trưởng hoặc suy giảm theo cấp số nhân (ví dụ: sự phân rã phóng xạ, sự tăng trưởng dân số).
- Tài chính: Tính lãi kép.
- Kỹ thuật: Tính toán các đại lượng trong các mạch điện, xử lý tín hiệu.
5. Bài Tập Luyện Tập
Để củng cố kiến thức, bạn có thể thực hành các bài tập sau:
| Bài tập | Đáp án |
|---|---|
| Tính 91/2 | 3 |
| Rút gọn biểu thức: (42 . 92)1/2 | 12 |
6. Lưu Ý Quan Trọng
Khi làm việc với lũy thừa với số mũ thực, cần lưu ý:
- Cơ số a phải lớn hơn 0.
- Các tính chất của lũy thừa chỉ áp dụng khi cơ số dương.
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về lý thuyết phép tính lũy thừa với số mũ thực trong chương trình Toán 11 Cánh Diều. Chúc bạn học tập tốt!