Bài 6 trang 104 Toán 11 tập 1 - Cánh Diều | Giải chi tiết & Chính xác

Bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều

Bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều: Giải tích

Bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình Giải tích, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các quy tắc tính đạo hàm và kỹ năng giải phương trình, bất phương trình.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán hiệu quả.

Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao cho \(AD = 3AM\). Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.

Đề bài

Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao cho \(AD = 3AM\). Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.

a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).

b) Chứng minh rằng MN song song với mặt phẳng (SCD) và NG song song với mặt phẳng (SAC).

Lời giải chi tiết

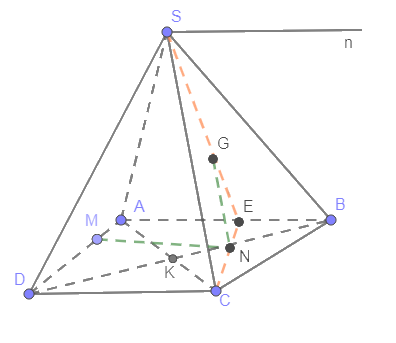
Bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều 1

+Ta có: \(KN = \frac{1}{3}KB = \frac{1}{6}DB\)

Tam giác DAB có: \(\frac{{DN}}{{DB}} = \frac{{DK + KN}}{{DB}} = \frac{{\frac{1}{2}DB + \frac{1}{6}DB}}{{DB}} = \frac{2}{3} = \frac{{DM}}{{DA}}\)

Theo Ta lét, suy ra MN // AB mà AB // CD

Suy ra MN // CD mà CD \( \subset \)(SCD) nên MN // (SCD).

+ Gọi E là trung điểm của AB

G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)

N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)

Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)

Bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn

Bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài 6 yêu cầu học sinh giải các bài tập liên quan đến việc tính đạo hàm của hàm số, tìm cực trị của hàm số và khảo sát hàm số. Cụ thể, bài tập có thể bao gồm:

Tính đạo hàm của hàm số y = f(x).
Tìm các điểm cực trị của hàm số y = f(x).
Khảo sát sự biến thiên của hàm số y = f(x).
Giải các phương trình, bất phương trình liên quan đến đạo hàm.

Lời giải chi tiết

Để giải bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều, học sinh cần nắm vững các kiến thức sau:

Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản như hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit.
Điều kiện cực trị: Biết điều kiện cần và đủ để hàm số có cực trị tại một điểm.
Khảo sát hàm số: Biết cách khảo sát sự biến thiên của hàm số bằng cách sử dụng đạo hàm.

Dưới đây là ví dụ về lời giải chi tiết cho một bài tập trong bài 6:

Ví dụ: Tính đạo hàm của hàm số y = x³ - 3x² + 2x - 1.

Lời giải:

y' = 3x² - 6x + 2

Hướng dẫn giải bài tập

Để giải các bài tập trong bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều, học sinh có thể làm theo các bước sau:

Đọc kỹ đề bài và xác định yêu cầu của bài tập.
Áp dụng các quy tắc tính đạo hàm để tính đạo hàm của hàm số.
Tìm các điểm cực trị của hàm số bằng cách giải phương trình y' = 0.
Khảo sát sự biến thiên của hàm số bằng cách xét dấu đạo hàm.
Kiểm tra lại kết quả và đảm bảo rằng đáp án của bạn là chính xác.

Mẹo giải bài tập

Để giải bài tập trong bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều một cách hiệu quả, học sinh có thể áp dụng các mẹo sau:

Sử dụng các công thức đạo hàm một cách linh hoạt.
Chú ý đến các điều kiện của bài toán.
Kiểm tra lại kết quả bằng cách thay các giá trị vào hàm số.

Tài liệu tham khảo

Học sinh có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều:

Sách giáo khoa Toán 11 tập 1 - Cánh Diều.
Sách bài tập Toán 11 tập 1 - Cánh Diều.
Các trang web học toán trực tuyến.

Kết luận: Bài 6 trang 104 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Bằng cách nắm vững các kiến thức và kỹ năng cần thiết, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.