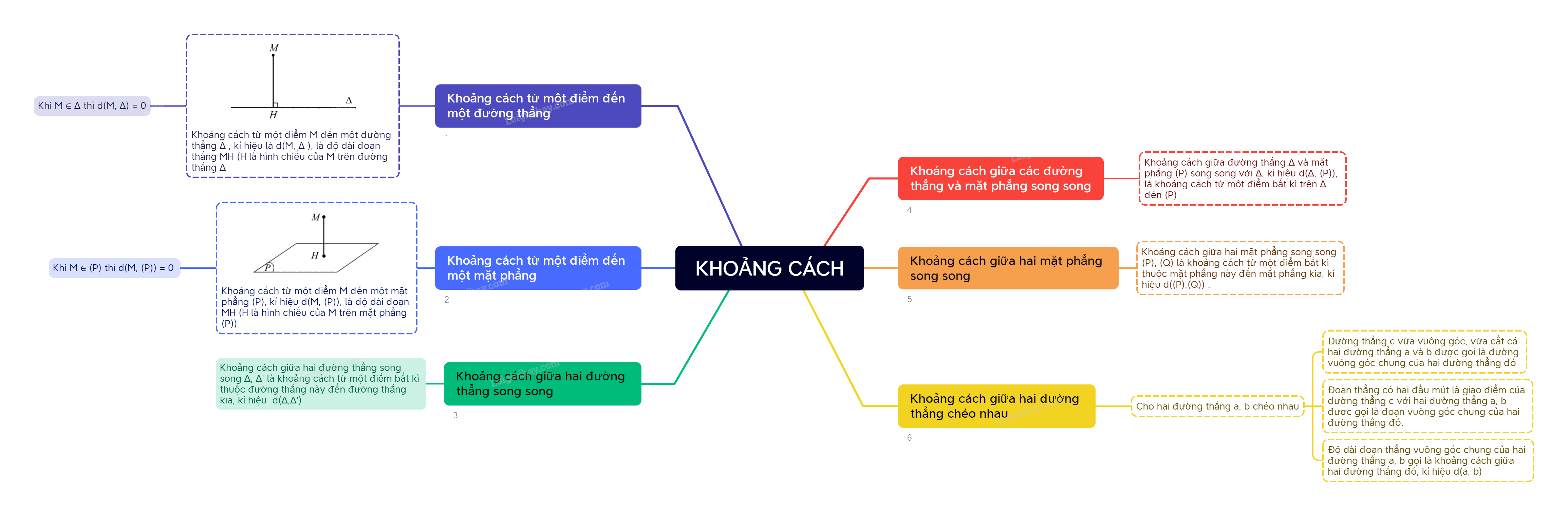
1. Khoảng cách từ một điểm đến một đường thẳng
Cho đường thẳng \(\Delta \) và điểm \(M\) không thuộc \(\Delta \). Gọi \(H\) là hình chiếu của điểm \(M\) trên đường thẳng \(\Delta \). Độ dài đoạn thẳng MH gọi là khoảng cách từ điểm \(M\) đến đường thẳng \(\Delta \), kí hiệu \(d(M,\Delta )\).
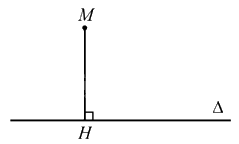
Chú ý: Khi điểm \(M\) thuộc đường thẳng \(\Delta \) thì \(d(M,\Delta ) = 0.\)
2. Khoảng cách từ một điểm đến một mặt phẳng
Cho mặt phẳng \((P)\) và điểm \(M\) không thuộc mặt phẳng \((P)\). Gọi \(H\) là hình chiếu của \(M\) trên mặt phẳng \((P)\). Độ dài đoạn thẳng MH gọi là khoảng cách từ điểm \(M\) đến mặt phẳng \((P)\), kí hiệu \(d(M,(P))\).
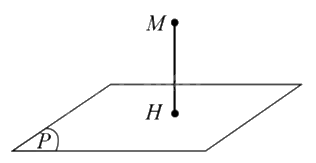
Chú ý: Khi điểm \(M\) thuộc mặt phẳng \((P)\) thì \(d(M,(P)) = 0.\)
3. Khoảng cách giữa hai đường thẳng song song
Khoảng cách giữa hai đường thẳng song song \(\Delta ,\Delta '\) là khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia, kí hiệu \(d\left( {\Delta ,{\Delta ^\prime }} \right)\).
Ví dụ: Trong hình dưới đây, ta có: \(d\left( {\Delta ,{\Delta ^\prime }} \right) = AB\) với \(A \in \Delta \), \(B \in {\Delta ^\prime },AB \bot \Delta ,AB \bot {\Delta ^\prime }\) và \(\Delta //{\Delta ^\prime }\).
4. Khoảng cách giữa đường thẳng và mặt phẳng song song
Cho đường thẳng \(\Delta \) song song với mặt phẳng \((P)\). Khoảng cách giữa đường thẳng \(\Delta \) và mặt phẳng \((P)\) là khoảng cách từ một điểm bất kì thuộc đường thẳng \(\Delta \) đến mặt phẳng \((P)\), kí hiệu \(d(\Delta ,(P))\).
Ví dụ: Trong hình dưới đây, ta có: \(d(\Delta ,(P)) = M{M^\prime } = h\), trong đó \(M \in \Delta ,{M^\prime } \in (P),M{M^\prime } \bot (P)\) và \(\Delta //(P)\).
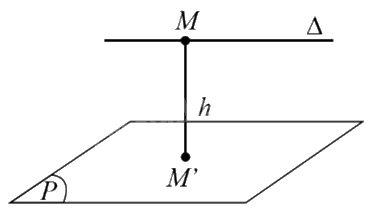
5. Khoảng cách giữa hai mặt phẳng song song
Khoảng cách giữa hai mặt phẳng song song \((P),(Q)\) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia, kí hiệu \(d((P),(Q))\).
Ví dụ: Trong hình dưới đây, ta có: \(d((P),(Q)) = IK = h\) với \(I \in (P),K \in (Q),IK \bot (P),IK \bot (Q)\) và \((P)//(Q)\).
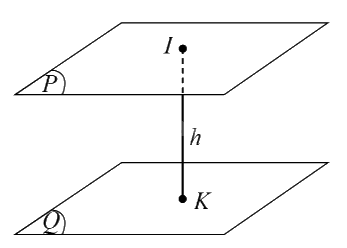
6. Khoảng cách giữa hai đưò̀ng thẳng chéo nhau
Cho hai đường thẳng a, b chéo nhau.
- Đường thẳng c vừa vuông góc, vừa cắt cả hai đường thẳng a và b được gọi là đường vuông góc chung của hai đường thẳng đó.
- Đoạn thẳng có hai đầu mút là giao điểm của đường thẳng c với hai đường thẳng a, b được gọi là đoạn vuông góc chung của hai đường thẳng đó.
- Độ dài đoạn thẳng vuông góc chung của hai đường thẳng a, b gọi là khoảng cách giữa hai đường thẳng đó, kí hiệu \(d(a,b)\).
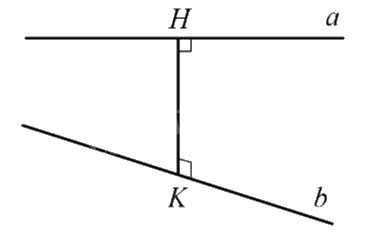
Ví dụ: Trong hình dưới đây, ta có: \(d(a,b) = HK\) với HK là đoạn vuông góc chung của \(a\) và \(b\).
