Bài 2 trang 99 SGK Toán 11 Tập 2 - Cánh Diều: Giải tích
Bài 2 trang 99 SGK Toán 11 Tập 2 - Cánh Diều thuộc chương trình Giải tích, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các quy tắc tính đạo hàm và kỹ năng giải phương trình, bất phương trình.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán hiệu quả.
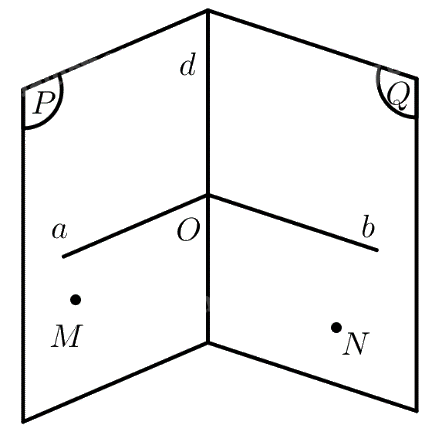
Chứng minh định lí sau: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Bài 2 trang 99 SGK Toán 11 Tập 2 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 2 trang 99 SGK Toán 11 Tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Đề bài:
Cho hàm số f(x) = x3 - 3x2 + 2. Tính f'(x) và tìm các điểm cực trị của hàm số.
Lời giải:
- Tính đạo hàm f'(x):
Sử dụng quy tắc đạo hàm của tổng và lũy thừa, ta có:
f'(x) = 3x2 - 6x
- Tìm các điểm cực trị:
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
- Xác định loại cực trị:
Ta xét dấu của f'(x) trên các khoảng:
- Khoảng (-∞, 0): Chọn x = -1, f'(-1) = 3(-1)2 - 6(-1) = 9 > 0, hàm số đồng biến.
- Khoảng (0, 2): Chọn x = 1, f'(1) = 3(1)2 - 6(1) = -3 < 0, hàm số nghịch biến.
- Khoảng (2, +∞): Chọn x = 3, f'(3) = 3(3)2 - 6(3) = 9 > 0, hàm số đồng biến.
Vậy:
- Tại x = 0, hàm số đạt cực đại, giá trị cực đại là f(0) = 2.
- Tại x = 2, hàm số đạt cực tiểu, giá trị cực tiểu là f(2) = 23 - 3(2)2 + 2 = -2.
Kết luận:
Hàm số f(x) = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Mở rộng và lưu ý:
- Để giải quyết các bài toán về cực trị, việc nắm vững các quy tắc tính đạo hàm và kỹ năng xét dấu đạo hàm là vô cùng quan trọng.
- Luôn kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số để xác nhận tính đúng đắn của lời giải.
- Bài tập này là một ví dụ điển hình về ứng dụng của đạo hàm trong việc tìm cực trị của hàm số, một kiến thức nền tảng trong chương trình Giải tích.
tusach.vn hy vọng với lời giải chi tiết này, các bạn học sinh có thể hiểu rõ hơn về Bài 2 trang 99 SGK Toán 11 Tập 2 - Cánh Diều và tự tin giải quyết các bài tập tương tự. Chúc các bạn học tốt!
| Giai đoạn | Hành động |
|---|
| Tính đạo hàm | f'(x) = 3x2 - 6x |
| Giải phương trình f'(x) = 0 | x = 0 hoặc x = 2 |
| Xác định loại cực trị | Cực đại tại x = 0, cực tiểu tại x = 2 |
| Bảng tóm tắt quá trình giải |