Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải mục 2 trang 62 SGK Toán 11 tập 2 - Cánh Diều
SGK Toán 11 - Cánh diều
Giải Toán 11 tập 2 - Cánh Diều
Chương VII. Đạo hàm
Bài 1. Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Giải mục 2 trang 62 SGK Toán 11 tập 2 - Cánh Diều

Giải mục 2 trang 62 SGK Toán 11 tập 2 - Cánh Diều

Tusach.vn xin giới thiệu lời giải chi tiết bài tập mục 2 trang 62 SGK Toán 11 tập 2, sách Cánh Diều. Bài viết này cung cấp đáp án chính xác, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, cập nhật nhanh chóng và đầy đủ nhất để hỗ trợ quá trình học tập của các em.

Cho hàm số y = f(x) có đồ thị (C), một điểm ({M_0}) cố định thuộc (C) có hoành độ ({x_0}).

Hoạt động 2Luyện tập – Vận dụng 3

Hoạt động 2

    Cho hàm số y = f(x) có đồ thị (C), một điểm \({M_0}\) cố định thuộc (C) có hoành độ \({x_0}\). Với mỗi điểm M thuộc (C) khác \({M_0}\), kí hiệu \({x_M}\) là hoành độ của điểm M và \({k_M}\) là hệ số góc của cát tuyến \({M_0}M\). Giả sử tồn tại giới hạn hữu hạn \({k_0} = \mathop {\lim }\limits_{{x_M} \to {x_0}} {k_M}\). Khi đó, ta coi đường thẳng \({M_0}T\) đi qua \({M_0}\) và có hệ số góc là \({k_0}\) là ví trị giới hạn của cát tuyến \({M_0}M\) khi điểm M di chuyển dọc theo (C) dần tới \({M_0}\) . Đường thẳng \({M_0}T\)được gọi là tiếp tuyến của (C) tại điểm \({M_0}\), còn \({M_0}\) được gọi là tiếp điểm (Hình 3).

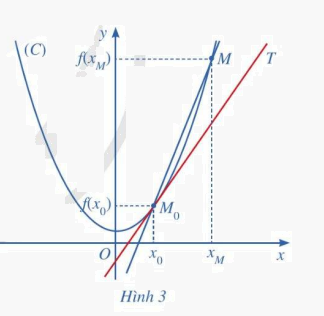
    Giải mục 2 trang 62 SGK Toán 11 tập 2 - Cánh Diều 1

    a) Xác định hệ số góc \({k_0}\) của tiếp tuyến \({M_0}T\) theo \({x_0}\)

    b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\)

    Phương pháp giải:

    Áp dụng định nghĩa đạo hàm để làm bài

    Lời giải chi tiết:

    a) \({k_0} = \mathop {\lim }\limits_{x \to {x_M}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}} = f'({x_0})\)

    b) Phương tình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\):

    \(y = {k_0}(x - {x_0}) + {y_0}\)

    Luyện tập – Vận dụng 3

      Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{1}{x}\) tại điểm N (1; 1)

      Phương pháp giải:

      Dựa vào ví dụ 3 để làm

      Lời giải chi tiết:

      - Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 có hệ số góc là:

      \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{x} - 1}}{{x - 1}} = - 1\)

      - Phương trình tiếp tuyến của đồ thị tại điểm N(1; 1) là:

      \(y = - 1.\left( {x - 1} \right) + 1 = - x + 1 + 1 = - x + 2\) \(\)

      Giải mục 2 trang 62 SGK Toán 11 tập 2 - Cánh Diều: Tổng quan và hướng dẫn chi tiết

      Mục 2 trang 62 SGK Toán 11 tập 2 Cánh Diều tập trung vào việc ôn tập và củng cố kiến thức về phép biến hình. Đây là một phần quan trọng trong chương trình học, giúp học sinh hiểu rõ hơn về các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững kiến thức này là nền tảng để giải quyết các bài toán hình học phức tạp hơn trong tương lai.

      Nội dung chính của Mục 2 trang 62

      • Ôn tập lý thuyết: Tóm tắt các định nghĩa, tính chất và công thức liên quan đến các phép biến hình.
      • Bài tập áp dụng: Các bài tập giúp học sinh rèn luyện kỹ năng nhận biết, phân tích và vận dụng các phép biến hình vào giải quyết các bài toán cụ thể.
      • Bài tập trắc nghiệm: Kiểm tra mức độ hiểu bài và khả năng làm bài nhanh của học sinh.

      Hướng dẫn giải chi tiết các bài tập trong Mục 2 trang 62

      Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 2 trang 62 SGK Toán 11 tập 2 Cánh Diều:

      Bài 1:

      (Đề bài cụ thể của bài 1)

      Lời giải:

      (Giải thích chi tiết từng bước giải bài 1, kèm theo hình vẽ minh họa nếu cần thiết)

      Bài 2:

      (Đề bài cụ thể của bài 2)

      Lời giải:

      (Giải thích chi tiết từng bước giải bài 2, kèm theo hình vẽ minh họa nếu cần thiết)

      Bài 3:

      (Đề bài cụ thể của bài 3)

      Lời giải:

      (Giải thích chi tiết từng bước giải bài 3, kèm theo hình vẽ minh họa nếu cần thiết)

      Mẹo giải bài tập về phép biến hình

      1. Xác định phép biến hình: Đọc kỹ đề bài để xác định phép biến hình nào được sử dụng trong bài toán.
      2. Tìm các yếu tố cần thiết: Xác định các yếu tố cần thiết để thực hiện phép biến hình, chẳng hạn như tâm quay, góc quay, vectơ tịnh tiến, trục đối xứng,...
      3. Áp dụng công thức: Sử dụng các công thức liên quan đến phép biến hình để tính toán và tìm ra kết quả.
      4. Kiểm tra lại kết quả: Sau khi giải xong bài toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

      Tài liệu tham khảo hữu ích

      Ngoài SGK Toán 11 tập 2 Cánh Diều, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về phép biến hình:

      • Sách bài tập Toán 11
      • Các trang web học toán trực tuyến
      • Các video bài giảng trên YouTube

      Kết luận

      Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trong Mục 2 trang 62 SGK Toán 11 tập 2 Cánh Diều, các em học sinh sẽ hiểu rõ hơn về phép biến hình và có thể tự tin giải quyết các bài toán liên quan. Chúc các em học tập tốt!

      Phép biến hìnhĐịnh nghĩaTính chất
      Phép tịnh tiếnBiến mỗi điểm thành một điểm sao cho vectơ nối hai điểm bằng một vectơ cho trước.Bảo toàn khoảng cách giữa hai điểm bất kỳ.
      Phép quayBiến mỗi điểm thành một điểm sao cho khoảng cách từ điểm đó đến tâm quay không đổi và góc giữa hai đoạn thẳng nối tâm quay với điểm cũ và điểm mới là một góc cho trước.Bảo toàn khoảng cách giữa hai điểm bất kỳ.

      Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

      CHỦ ĐỀ SÁCH XEM NHIỀU

      Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

      VỀ TUSACH.VN