Giải Mục 3 Trang 70, 71 SGK Toán 11 Tập 1 - Cánh Diều
Chào mừng bạn đến với lời giải chi tiết Mục 3 trang 70, 71 SGK Toán 11 tập 1 - Cánh Diều trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc nội dung bài học và tự tin giải quyết các bài tập tương tự.
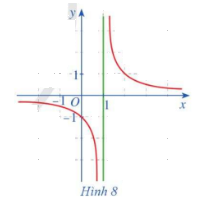
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\,\,\left( {x \ne 1} \right)\) có đồ thị như ở Hình 8. Quan sát đồ thị đó và cho biết:
a) Khi biến x dần tới 1 về bên phải thì \(f\left( x \right)\) dần tới đâu.
b) Khi biến x dần tới 1 về bên trái thì \(f\left( x \right)\) dần tới đâu
Giải Mục 3 Trang 70, 71 SGK Toán 11 Tập 1 - Cánh Diều: Tổng Quan và Phương Pháp Giải Chi Tiết
Mục 3 trang 70, 71 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình học về Hàm số bậc hai. Đây là một phần quan trọng trong chương trình Toán 11, đặt nền móng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Việc nắm vững kiến thức và kỹ năng giải các bài tập trong mục này là vô cùng cần thiết.
Nội Dung Chính của Mục 3
Mục 3 tập trung vào việc:
- Xác định các hệ số a, b, c của hàm số bậc hai y = ax2 + bx + c.
- Tìm tập xác định của hàm số.
- Xác định đỉnh, trục đối xứng và các điểm đặc biệt của parabol.
- Vẽ đồ thị hàm số bậc hai.
- Ứng dụng đồ thị hàm số bậc hai để giải các bài toán thực tế.
Các Dạng Bài Tập Thường Gặp
Trong Mục 3, học sinh thường gặp các dạng bài tập sau:
- Bài tập xác định hệ số: Yêu cầu xác định các hệ số a, b, c của hàm số bậc hai khi cho dạng tổng quát hoặc thông tin về đồ thị.
- Bài tập tìm đỉnh, trục đối xứng: Yêu cầu tìm tọa độ đỉnh và phương trình trục đối xứng của parabol.
- Bài tập vẽ đồ thị: Yêu cầu vẽ đồ thị hàm số bậc hai dựa trên các thông tin đã cho.
- Bài tập ứng dụng: Yêu cầu giải các bài toán thực tế liên quan đến hàm số bậc hai, ví dụ như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
Hướng Dẫn Giải Chi Tiết Bài Tập
Để giải các bài tập trong Mục 3, bạn cần nắm vững các công thức và phương pháp sau:
- Công thức tính tọa độ đỉnh: xđỉnh = -b/2a, yđỉnh = -Δ/4a (với Δ = b2 - 4ac).
- Phương trình trục đối xứng: x = -b/2a.
- Cách vẽ đồ thị: Xác định đỉnh, trục đối xứng, các điểm đặc biệt (giao điểm với trục Oy, giao điểm với trục Ox nếu có), sau đó vẽ parabol.
Ví dụ Minh Họa
Bài tập: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh và phương trình trục đối xứng.
Giải:
Hệ số a = 1, b = -4, c = 3.
Tọa độ đỉnh: xđỉnh = -(-4)/(2*1) = 2, yđỉnh = -( (-4)2 - 4*1*3 )/(4*1) = -(-4)/4 = 1. Vậy đỉnh là (2; 1).
Phương trình trục đối xứng: x = 2.
Lưu Ý Quan Trọng
Khi giải các bài tập về hàm số bậc hai, bạn cần chú ý:
- Xác định đúng hệ số a, b, c.
- Sử dụng đúng công thức tính tọa độ đỉnh và phương trình trục đối xứng.
- Vẽ đồ thị chính xác, chú ý đến hình dạng của parabol (lõm lên hay lõm xuống).
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng Hành Cùng Bạn Trên Con Đường Học Tập
Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 1 - Cánh Diều. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Chúc bạn học tập tốt!
