Bài 2 trang 119 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Bài 2 trang 119 SGK Toán 11 tập 1 - Cánh Diều
Bài 2 thuộc chương trình học Toán 11 tập 1, sách Cánh Diều, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tính toán và chứng minh các giới hạn, đồng thời hiểu rõ ý nghĩa của giới hạn trong thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình hộp ABCD.A’B’C’D. Xác định ảnh của tam giác A’C’D’qua phép chiếu song song lên mặt phẳng (ABCD) theo phương A’B.
Đề bài
Cho hình hộp ABCD.A’B’C’D. Xác định ảnh của tam giác A’C’D’qua phép chiếu song song lên mặt phẳng (ABCD) theo phương A’B.
Phương pháp giải - Xem chi tiết
Dựa vào các tính chất của phép chiếu song song để xác định ảnh của tam giác A’C’D’qua phép chiếu song song lên mặt phẳng (ABCD) theo phương A’B.
Lời giải chi tiết
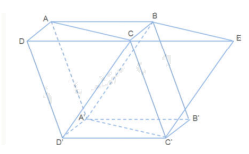
Ta có: B là ảnh của A’ lên (ABCD)
Ta có: D’C // A’B nên C là ảnh của D’ lên (ABCD)
Từ C’ kẻ C’E // CD’ // A’B
Suy ra E là ảnh của C‘ lên (ABCD)
Vậy tam giác BCE là ảnh của tam giác A’C’D’ qua phép chiếu song song lên mặt phẳng (ABCD) theo phương A’B
Bài 2 trang 119 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 2 trang 119 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học về giới hạn của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các kỹ năng tính toán giới hạn.
Nội dung bài tập
Bài 2 thường yêu cầu học sinh tính giới hạn của một hàm số khi x tiến tới một giá trị cụ thể. Các hàm số có thể là đa thức, phân thức, hoặc các hàm số phức tạp hơn. Để giải bài tập, học sinh có thể sử dụng các phương pháp sau:
- Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào hàm số để tính giới hạn. Phương pháp này chỉ áp dụng được khi hàm số liên tục tại điểm x.
- Phương pháp phân tích: Phân tích hàm số thành các nhân tử hoặc sử dụng các phép biến đổi đại số để đơn giản hóa hàm số trước khi tính giới hạn.
- Phương pháp sử dụng định lý giới hạn: Áp dụng các định lý giới hạn để tính giới hạn của hàm số.
Giải chi tiết Bài 2 trang 119 SGK Toán 11 tập 1 - Cánh Diều
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau giải chi tiết một ví dụ cụ thể. Giả sử bài tập yêu cầu tính giới hạn của hàm số f(x) = (x^2 - 1) / (x - 1) khi x tiến tới 1.
- Bước 1: Phân tích hàm số thành các nhân tử: f(x) = (x - 1)(x + 1) / (x - 1)
- Bước 2: Rút gọn hàm số: f(x) = x + 1 (với x ≠ 1)
- Bước 3: Tính giới hạn: lim (x→1) f(x) = lim (x→1) (x + 1) = 1 + 1 = 2
Vậy, giới hạn của hàm số f(x) khi x tiến tới 1 là 2.
Lưu ý khi giải bài tập về giới hạn
- Luôn kiểm tra xem hàm số có liên tục tại điểm x hay không trước khi áp dụng phương pháp trực tiếp.
- Sử dụng các phép biến đổi đại số một cách cẩn thận để tránh sai sót.
- Nắm vững các định lý giới hạn và áp dụng chúng một cách linh hoạt.
Ứng dụng của giới hạn trong thực tế
Giới hạn là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong thực tế, chẳng hạn như:
- Tính vận tốc tức thời: Vận tốc tức thời của một vật tại một thời điểm nhất định được tính bằng giới hạn của vận tốc trung bình khi khoảng thời gian tiến tới 0.
- Tính đạo hàm: Đạo hàm của một hàm số tại một điểm được định nghĩa bằng giới hạn của tỷ số giữa độ biến thiên của hàm số và độ biến thiên của biến số khi độ biến thiên của biến số tiến tới 0.
- Tính diện tích: Diện tích của một hình phẳng được tính bằng giới hạn của tổng diện tích các hình chữ nhật nhỏ khi số lượng hình chữ nhật tiến tới vô cùng.
Kết luận: Bài 2 trang 119 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về giới hạn của hàm số. Bằng cách nắm vững các khái niệm cơ bản, các định lý liên quan và các kỹ năng tính toán giới hạn, học sinh có thể tự tin giải bài tập này và áp dụng kiến thức vào thực tế.
Tìm kiếm thêm:
- Tusach.vn - Giải bài tập Toán 11
- Giải Toán 11 Cánh Diều