Đề bài
Với giả thiết ở Bài tập 4, hãy:
a) Chứng minh rằng \(BC\parallel \left( {SAD} \right)\) và tính khoảng cách giữa \(BC\) và mặt phẳng \(\left( {SAD} \right)\).
b) Chứng minh rằng \(BD \bot \left( {SAC} \right)\) và tính khoảng cách giữa hai đường thẳng \(BD\) và \(SC\).
Phương pháp giải - Xem chi tiết
‒ Cách chứng minh đường thẳng song song với mặt phẳng: Chứng minh đường thẳng đó song song với một đường thẳng nằm trên mặt phẳng.
‒ Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song: Tính khoảng cách từ một điểm trên đường thẳng đến mặt phẳng.
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng: Chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trên mặt phẳng.
‒ Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.
Lời giải chi tiết
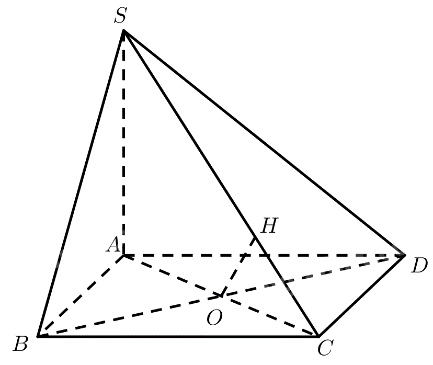
a) \(ABCD\) là hình vuông \( \Rightarrow BC\parallel A{\rm{D}}\)
Mà \(A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\)
\( \Rightarrow BC\parallel \left( {SAD} \right) \Rightarrow d\left( {BC,\left( {SAD} \right)} \right) = d\left( {B,\left( {SAD} \right)} \right)\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\)
\(ABCD\) là hình vuông \( \Rightarrow AB \bot A{\rm{D}}\)
\( \Rightarrow AB \bot \left( {SA{\rm{D}}} \right) \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\)
Vậy \(d\left( {BC,\left( {SAD} \right)} \right) = a\).
b) \(ABCD\) là hình vuông \( \Rightarrow B{\rm{D}} \bot A{\rm{C}}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot B{\rm{D}}\)
\( \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\)
Gọi \(O = AC \cap B{\rm{D}}\), kẻ \(OH \bot SC\left( {H \in SC} \right)\)
\(B{\rm{D}} \bot \left( {SAC} \right) \Rightarrow B{\rm{D}} \bot OH\)
\( \Rightarrow d\left( {B{\rm{D}},SC} \right) = OH\)
\(\Delta ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OC = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)
\(\Delta SAC \backsim \Delta OHC\,(g.g) \Rightarrow \frac{{SA}}{{OH}} = \frac{{SC}}{{OC}} \Rightarrow OH = \frac{{SA.OC}}{{SC}} = \frac{{a\sqrt 6 }}{6}\)
Vậy \(d\left( {B{\rm{D}},SC} \right) = \frac{{a\sqrt 6 }}{6}\).
