Giải mục 1 trang 73, 74, 75 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Giải mục 1 trang 73, 74, 75 SGK Toán 11 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 73, 74, 75 SGK Toán 11 tập 1 chương trình Cánh Diều. Bài viết này sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những tài liệu và lời giải chính xác, dễ hiểu nhất.
Quan sát đồ thị hàm số (fleft( x right) = x) ở Hình 11. a) Tính (mathop {lim }limits_{x to 1} fleft( x right).) b) So sánh (mathop {lim }limits_{x to 1} fleft( x right)) với (fleft( 1 right).)
HĐ 1
Quan sát đồ thị hàm số \(f\left( x \right) = x\) ở Hình 11.
a) Tính \(\mathop {\lim }\limits_{x \to 1} f\left( x \right).\)
b) So sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) với \(f\left( 1 \right).\)
Phương pháp giải:
Sử dụng \(\mathop {\lim }\limits_{x \to {x_0}} x = {x_0}\)
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} x = 1\)
b) \(f\left( 1 \right) = 1 \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right).\)
LT - VD 1
Xét tính liên tục của hàm số \(f\left( x \right) = {x^3} + 1\) tại \({x_0} = 1.\)
Phương pháp giải:
Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải chi tiết:
Ta có \(f\left( {{x_0}} \right) = f\left( 1 \right) = {1^3} + 1 = 2;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^3} + 1} \right) = \mathop {\lim }\limits_{x \to 1} {x^3} + 1 = 1 + 1 = 2\)
\( \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0} = 1.\)
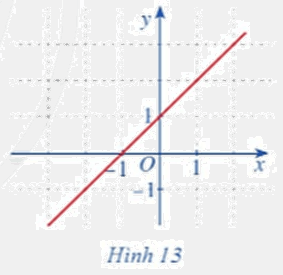
HĐ 2
Cho hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}.\)
a) Giả sử \({x_0} \in \mathbb{R}.\) Hàm số \(f\left( x \right)\) có liên tục tại điểm \({x_0}\) hay không?
b) Quan sát đồ thị hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}\) (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.

Phương pháp giải:
Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải chi tiết:
a) Ta có \(f\left( {{x_0}} \right) = {x_0} + 1;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to {x_0}} x + 1 = {x_0} + 1\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0}.\)
b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị \(x \in \mathbb{R}.\)
LT - VD 2
Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x - 1,\,\,x < 2\\ - x,\,\,x \ge 2\end{array} \right.\) có liên tục trên \(\mathbb{R}\) hay không?
Phương pháp giải:
- Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
- \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L\)
Lời giải chi tiết:
+) Với mỗi \({x_0} \in \left( { - \infty ;2} \right)\) có \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x - 1} \right) = {x_0} - 1 = f\left( {{x_0}} \right)\)
Do đó hàm số \(f\left( x \right)\) liên tục tại \({x_0} \in \left( { - \infty ;2} \right).\)
+) Với mỗi \({x_0} \in \left( {2; + \infty } \right)\) có \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( { - x} \right) = - {x_0} = f\left( {{x_0}} \right)\)
Do đó hàm số \(f\left( x \right)\) liên tục tại \({x_0} \in \left( {2; + \infty } \right).\)
+) Với mỗi \({x_0} = 2\) có \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {x - 1} \right) = 2 - 1 = 1;\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - x} \right) = - 2\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\) do đó không tồn tại \(\mathop {\lim }\limits_{x \to 2} f\left( x \right).\)
Vậy hàm số \(f\left( x \right)\) gián đoạn tại \({x_0} = 2\) nên hàm số \(f\left( x \right)\) không liên tục trên \(\mathbb{R}.\)
Giải mục 1 trang 73, 74, 75 SGK Toán 11 tập 1 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 1 của chương trình Toán 11 tập 1 Cánh Diều tập trung vào việc giới thiệu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, mở đầu cho chương trình Giải tích. Việc nắm vững kiến thức về giới hạn sẽ giúp học sinh hiểu sâu hơn về các khái niệm tiếp theo như đạo hàm, tích phân.
Nội dung chính của Mục 1
- Khái niệm giới hạn của hàm số tại một điểm: Hàm số f(x) có giới hạn L khi x tiến tới a nếu với mọi số dương ε (epsilon) nhỏ tùy ý, tồn tại một số dương δ (delta) sao cho nếu 0 < |x - a| < δ thì |f(x) - L| < ε.
- Tính chất của giới hạn: Tổng, hiệu, tích, thương của các giới hạn (khi mẫu khác 0).
- Các dạng giới hạn cơ bản: Giới hạn của các hàm đa thức, hàm phân thức, hàm lượng giác.
- Ứng dụng của giới hạn: Tính giới hạn của hàm số, xét tính liên tục của hàm số.
Giải chi tiết các bài tập trang 73, 74, 75
Dưới đây là lời giải chi tiết cho từng bài tập trong SGK Toán 11 tập 1 Cánh Diều trang 73, 74, 75:
Bài 1 (Trang 73)
Nội dung bài tập: Tính các giới hạn sau: a) lim (x→2) (x^2 + 1); b) lim (x→-1) (3x - 2); c) lim (x→0) (x + 5)
Lời giải:
- a) lim (x→2) (x^2 + 1) = 2^2 + 1 = 5
- b) lim (x→-1) (3x - 2) = 3*(-1) - 2 = -5
- c) lim (x→0) (x + 5) = 0 + 5 = 5
Bài 2 (Trang 74)
Nội dung bài tập: Tính các giới hạn sau: a) lim (x→3) (x^2 - 9)/(x - 3); b) lim (x→1) (x^3 - 1)/(x - 1)
Lời giải:
- a) lim (x→3) (x^2 - 9)/(x - 3) = lim (x→3) (x - 3)(x + 3)/(x - 3) = lim (x→3) (x + 3) = 6
- b) lim (x→1) (x^3 - 1)/(x - 1) = lim (x→1) (x - 1)(x^2 + x + 1)/(x - 1) = lim (x→1) (x^2 + x + 1) = 3
Bài 3 (Trang 75)
Nội dung bài tập: Cho hàm số f(x) = (x^2 - 4)/(x - 2). Tính lim (x→2) f(x).
Lời giải:
lim (x→2) f(x) = lim (x→2) (x^2 - 4)/(x - 2) = lim (x→2) (x - 2)(x + 2)/(x - 2) = lim (x→2) (x + 2) = 4
Lưu ý khi giải bài tập về giới hạn
- Luôn kiểm tra xem mẫu số có bằng 0 hay không khi x tiến tới một giá trị cụ thể.
- Sử dụng các tính chất của giới hạn để đơn giản hóa biểu thức.
- Áp dụng các dạng giới hạn cơ bản để tính toán nhanh chóng.
Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về Mục 1 SGK Toán 11 tập 1 Cánh Diều và tự tin giải các bài tập tương tự. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi tại tusach.vn nhé!