Bài 5 trang 94 SGK Toán 11 tập 2 - Cánh diều
Tổng quan nội dung
Bài 5 trang 94 SGK Toán 11 tập 2 - Cánh Diều
Bài 5 trang 94 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, các phép biến đổi lượng giác và giải phương trình lượng giác để giải quyết các bài toán cụ thể.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
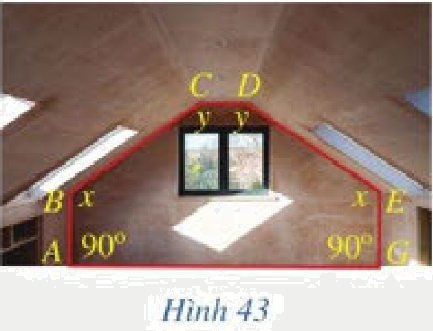
Trong Hình 43, xét các góc nhị diện có góc phẳng nhị diện tương ứng là \(\widehat B,\widehat C,\widehat D,\widehat E\) trong cùng mặt phẳng.
Đề bài
Trong Hình 43, xét các góc nhị diện có góc phẳng nhị diện tương ứng là \(\widehat B,\widehat C,\widehat D,\widehat E\) trong cùng mặt phẳng. Lục giác \(ABCDEG\) nằm trong mặt phẳng đó có \(AB = GE = 2{\rm{ }}m,BC = DE,\widehat A = \widehat G = {90^ \circ },\widehat B = \widehat E = x,\widehat C = \widehat D = y\). Biết rằng khoảng cách từ \(C\) và \({\rm{D}}\) đến \({\rm{AG}}\) là \(4{\rm{ }}m\), \(AG = 12{\rm{ }}m,CD = 1{\rm{ }}m\). Tìm x, y (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).
Lời giải chi tiết
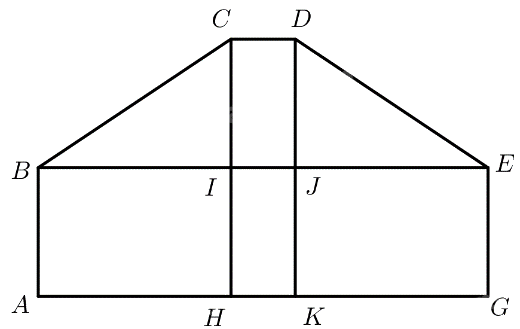
Kẻ \(CH \bot AG\left( {H \in AG} \right),DK \bot AG\left( {K \in AG} \right)\)
Gọi \(I = BE \cap CH,J = BE \cap DK\).
\(ABEG\) là hình chữ nhật \( \Rightarrow BE = AB = 12\)
\(C{\rm{D}}KH,C{\rm{D}}JI\) là hình chữ nhật \( \Rightarrow HK = IJ = C{\rm{D}} = 1\)
\(ABIH,EGKJ\) là hình chữ nhật \( \Rightarrow IH = JK = AB = 2\)
\(AH = GK = BI = EJ = \frac{{AG - HK}}{2} = \frac{{12 - 1}}{2} = 5,5\)
\(CH = d\left( {C,AG} \right) = 4 \Rightarrow CI = CH - IH = 4 - 2 = 2\)
\(\Delta BCI\) vuông tại \(I\)\( \Rightarrow \tan \widehat {CBI} = \frac{{CI}}{{BI}} = \frac{2}{{5,5}} = \frac{4}{{11}} \Rightarrow \widehat {CBI} \approx 19,{98^ \circ }\)
\(\begin{array}{l} \Rightarrow x = \widehat {ABI} + \widehat {CBI} = {90^ \circ } + 19,{98^ \circ } = 110,{0^ \circ }\\ \Rightarrow y = {180^ \circ } - x = {180^ \circ } - 110,{0^ \circ } = 70,{0^ \circ }\end{array}\)
Bài 5 trang 94 SGK Toán 11 tập 2 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 5 trang 94 SGK Toán 11 tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số lượng giác và các ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 5 yêu cầu giải các phương trình lượng giác sau:
- sin(x + π/3) = sin(π/6)
- cos(2x - π/4) = cos(π/3)
- tan(x - π/6) = tan(π/4)
- cot(3x + π/2) = cot(π/5)
Lời giải chi tiết
Để giải các phương trình lượng giác này, chúng ta cần sử dụng các công thức lượng giác cơ bản và các phương pháp giải phương trình lượng giác đã học.
Giải phương trình sin(x + π/3) = sin(π/6)
Phương trình tương đương với:
- x + π/3 = π/6 + k2π (k ∈ Z)
- x + π/3 = π - π/6 + k2π (k ∈ Z)
Giải hai phương trình trên, ta được:
- x = -π/6 + k2π (k ∈ Z)
- x = 5π/6 + k2π (k ∈ Z)
Giải phương trình cos(2x - π/4) = cos(π/3)
Phương trình tương đương với:
- 2x - π/4 = π/3 + k2π (k ∈ Z)
- 2x - π/4 = -π/3 + k2π (k ∈ Z)
Giải hai phương trình trên, ta được:
- x = 7π/24 + kπ (k ∈ Z)
- x = -π/24 + kπ (k ∈ Z)
Giải phương trình tan(x - π/6) = tan(π/4)
Phương trình tương đương với:
x - π/6 = π/4 + kπ (k ∈ Z)
Giải phương trình trên, ta được:
x = 5π/12 + kπ (k ∈ Z)
Giải phương trình cot(3x + π/2) = cot(π/5)
Phương trình tương đương với:
3x + π/2 = π/5 + kπ (k ∈ Z)
Giải phương trình trên, ta được:
x = -3π/30 + kπ/3 = -π/10 + kπ/3 (k ∈ Z)
Lưu ý khi giải bài tập
- Luôn kiểm tra điều kiện xác định của hàm số lượng giác.
- Sử dụng đúng các công thức lượng giác cơ bản.
- Biết cách biến đổi phương trình lượng giác về dạng đơn giản để dễ dàng giải.
Tầm quan trọng của việc luyện tập
Việc luyện tập thường xuyên các bài tập về hàm số lượng giác là rất quan trọng để nắm vững kiến thức và rèn luyện kỹ năng giải toán. Hãy làm thêm nhiều bài tập tương tự để nâng cao khả năng của bản thân.
tusach.vn hy vọng với lời giải chi tiết này, các bạn học sinh có thể hiểu rõ hơn về Bài 5 trang 94 SGK Toán 11 tập 2 - Cánh Diều và tự tin giải các bài tập tương tự. Chúc các bạn học tốt!