Giải mục 1 trang 48, 49, 50 SGK Toán 11 tập 2 - Cánh Diều

Trong bài toán ở phần mở đầu, giả sử r = 1,14%/năm

a) Viết phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu

b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lũy thừa?

Phương pháp giải:

Dựa vào công thức đã tìm được ở bài mở đầu rồi tính

Lời giải chi tiết:

a) ­­­Phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu là:

\(S = 2S.{e^{1,14.t}} \Leftrightarrow 2{e^{1,14t}} = 1 \Leftrightarrow {e^{1,14t}} = \frac{1}{2}\)

b) Phương trình vừa tìm được có ẩn là t và nằm ở vị trí mũ của lũy thừa

Cho hai ví dụ về phương trình mũ

Phương pháp giải:

Dựa vào kiến thức vừa học để xác định phương trình mũ

Lời giải chi tiết:

2 ví dụ về phương trình mũ

1. \({4^{x + 1}} = 2\)
2. \({7^{2x}} = 49\)

a) Vẽ đồ thị hàm số \(y = {3^x}\) và đường thẳng y = 7

b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({3^x} = 7\)

Phương pháp giải:

Dựa vào kiến thức đã học ở bài trước để vẽ đồ thị

Lời giải chi tiết:

a) Ta có bảng sau:

Ta có đồ thị sau:

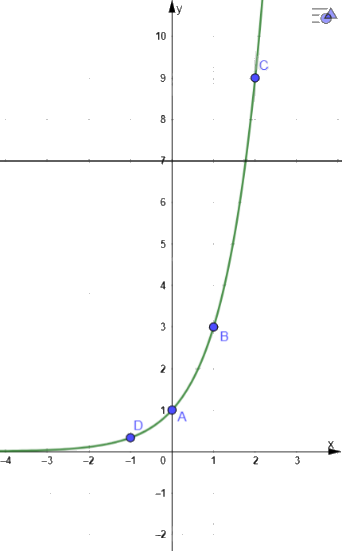
b, Hai đồ thị \(y = {3^x}\) và y = 7 có 1 giao điểm. Vậy số nghiệm của phương trình \({3^x} = 7\) là 1

Giải mỗi phương trình sau:

a) \({9^{16 - x}} = {27^{x + 4}}\)

b) \({16^{x - 2}} = 0,{25.2^{ - x + 4}}\)

Phương pháp giải:

Dựa vào kiến thức vừa học về phương trình mũ để giải

Lời giải chi tiết:

a) \({9^{16 - x}} = {27^{x + 4}}\)

\(\begin{array}{l} \Leftrightarrow {3^{2.\left( {16 - x} \right)}} = {3^{3.\left( {x + 4} \right)}}\\ \Leftrightarrow 2.\left( {16 - x} \right) = 3.\left( {x + 4} \right)\\ \Leftrightarrow 32 - 2x - 3x - 12 = 0\\ \Leftrightarrow - 5x = - 20\\ \Leftrightarrow x = 4\end{array}\)

b) \({16^{x - 2}} = 0,{25.2^{ - x + 4}}\)

\(\begin{array}{l} \Leftrightarrow {2^{4\left( {x - 2} \right)}} = 0,{25.2^{ - x + 4}}\\ \Leftrightarrow {2^{4x - 8 + x - 4}} = 0,25\\ \Leftrightarrow {2^{5x - 12}} = 0,25\\ \Leftrightarrow 5x - 12 = {\log _2}0,25\\ \Leftrightarrow 5x - 12 = - 2\\ \Leftrightarrow x = 2\end{array}\)

Chỉ số hay độ pH của một dung dịch được tính theo công thức: \(pH = - \log [{H^ + }]\) (Trong đó \([{H^ + }]\) chỉ nống độ hydrogen). Đo chỉ số pH của một mẫu nước sông, ta có kết quả là pH = 6,1.

a) Viết phương trình thể hiện nồng độ x của ion hydrogen \([{H^ + }]\) trong mẫu nước sông đó.

b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?

Phương pháp giải:

Dựa vào công thức tính pH để biểu diễn

Lời giải chi tiết:

a) Ta có: \( - \log [{H^ + }] = 6.1 \Leftrightarrow - \log x = 6,1\)

b) Phương trình vừa tìm được có ẩn là x và nằm ở vị trí hệ số của logarit

Cho hai ví dụ về phương trình logarit

Phương pháp giải:

Dựa vào dạng phương trình logarit vừa học để làm

Lời giải chi tiết:

1. \({\log _2}\left( {x + 1} \right) = 8\)
2. \({\log _3}\left( {{x^2} + x + 1} \right) = 2\)

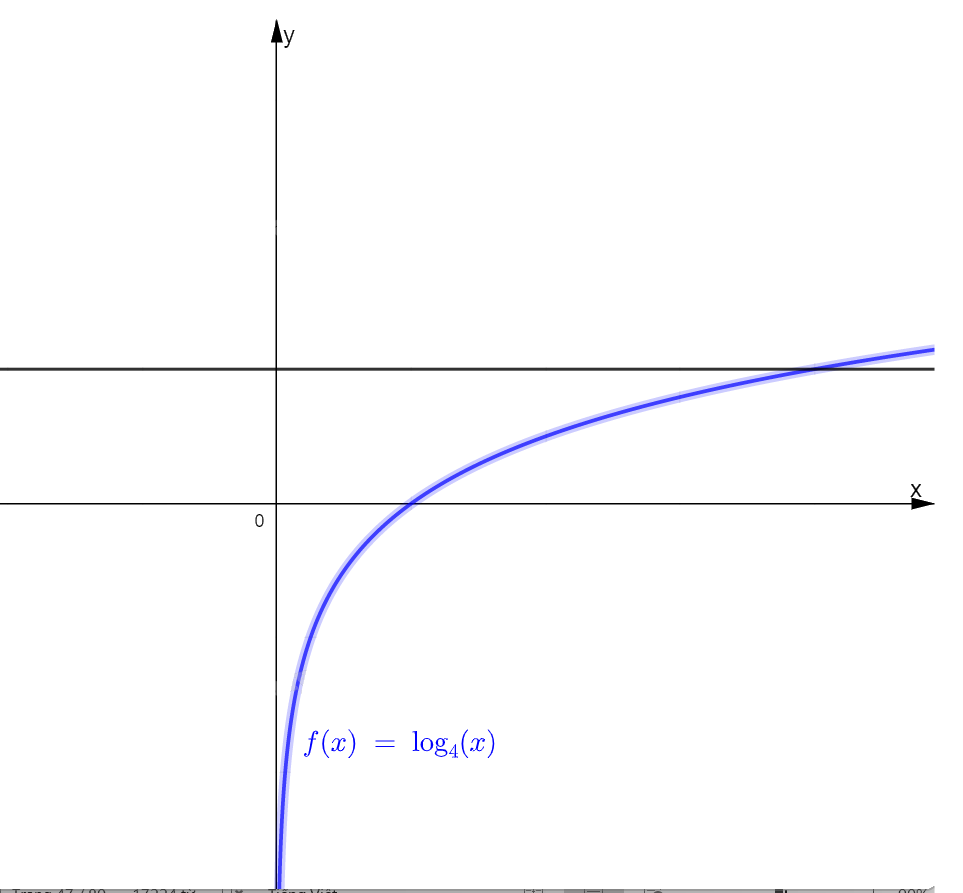
a) Vẽ đồ thị hàm số \(y = {\log _4}x\) và đường thẳng y = 5

b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({\log _4}x = 5\)

Phương pháp giải:

Dựa vào cách vẽ đồ thị ở bài trên để vẽ hàm

Lời giải chi tiết:

a) Đồ thị hai hàm số:

b, Hai hàm số có 1 giao điểm. Phương trình \({\log _4}x = 5\) có 1 nghiệm­

Giải mỗi phương trình sau:

a) \({\log _5}\left( {2x - 4} \right) + {\log _{\frac{1}{5}}}\left( {x - 1} \right) = 0\).

b) \({\log _2}x + {\log _4}x = 3\).

Phương pháp giải:

Dựa vào công thức vừa học để giải phương trình.

Lời giải chi tiết:

a) \({\log _5}\left( {2x - 4} \right) + {\log _{\frac{1}{5}}}\left( {x - 1} \right) = 0\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x > 2\\{\log _5}\left( {2x - 4} \right) - {\log _5}\left( {x - 1} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 2\\{\log _5}\left( {\frac{{2x - 4}}{{x - 1}}} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 2\\\frac{{2x - 4}}{{x - 1}} = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 2\\2x - 4 = x - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 2\\x = 3\end{array} \right.\\ \Leftrightarrow x = 3\end{array}\)

Vậy phương trình có nghiệm x = 3.

b) \({\log _2}x + {\log _4}x = 3\)

\(\begin{array}{*{20}{l}}\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > 0}\\{{{\log }_2}x + {{\log }_{{2^2}}}x = 3}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > 0}\\{{{\log }_2}x + \frac{1}{2}{{\log }_2}x = 3}\end{array}} \right.\end{array}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > 0}\\{\frac{3}{2}{{\log }_2}x = 3}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > 0}\\{{{\log }_2}x = 2}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > 0}\\{x = 4}\end{array}} \right.}\\{ \Leftrightarrow x = 4}\end{array}\)

Vậy phương trình có nghiệm x = 4.