Bài 9 trang 120 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Bài 9 trang 120 SGK Toán 11 tập 1 - Cánh Diều
Bài 9 thuộc chương trình Toán 11 tập 1, sách Cánh Diều, tập trung vào việc ôn tập chương 1: Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, tích vô hướng, và ứng dụng của vectơ để giải quyết các bài toán hình học.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập Toán 11 hiệu quả.
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của AB, C’D’.
Đề bài
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của AB, C’D’.
a) Chứng minh rằng (A’DN) // (B’CM)
b) Gọi E, F lần lượt là giao điểm của đường thẳng D’B với các mặt phẳng (A’DN), (B’CM). Chứng minh rằng \(D'E = BF = \frac{1}{2}EF\)
Phương pháp giải - Xem chi tiết
Nếu d,d' nằm trong (P) và d, d'//(Q) thì (P)//(Q).
Lời giải chi tiết
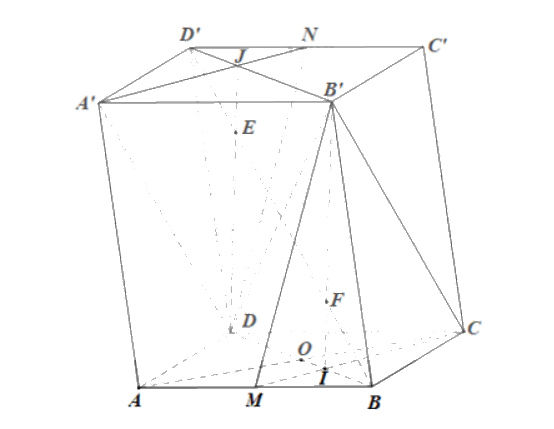
a)
Ta có: (ADD’A’) // (CBC’B’);
(ADD’A’) ∩ (DCB’A’) = A’D;
(CBC’B’) ∩ (DCB’A’) = B’C.
Do đó A’D // B’C, mà B’C ⊂ (B’CM) nên A’D // (B’CM).
Tương tự: (ABB’A’) // (DCC’D’);
(ABB’A’) ∩ (DMB’N) = MB’;
(DCC’D’) ∩ (DMB’N) = DN.
Do đó MB’ // DN, mà MB’ ⊂ (B’CM) nên DN // (B’CM).
Ta có: A’D // (B’CM);
DN // (B’CM);
A’D, DN cắt nhau tại điểm D và cùng nằm trong mp(A’DN)
Do đó (A’DN) // (B’CM).
b)
Trong mp(A’B’C’D’), gọi J là giao điểm của A’N và B’D’.
Trong mp(BDD’B’), D’B cắt DJ tại E.
Ta có: D’B ∩ DJ = {E} mà DJ ⊂ (A’DN) nên E là giao điểm của D’B và (A’DN).
Tương tự, trong mp(ABCD), gọi I là giao điểm của CM và BD.
Trong mp(BDD’B’), D’B cắt B’I tại F.
Ta có: D’B ∩ B’I = {F} mà B’I ⊂ (B’CM) nên F là giao điểm của D’B và (B’CM).
• Ta có: (A’DN) // (B’CM);
(A’DN) ∩ (BDD’B’) = DJ;
(B’CM) ∩ (BDD’B’) = B’I.
Do đó DJ // B’I.
Trong mp(BDD’B’), xét DBDE có IF // DE nên theo định lí Thalès ta có: \(\frac{{BI}}{{BD}} = \frac{{BF}}{{BE}}\) (1)
Trong mp(ABCD), gọi O là giao điểm của hai đường chéo AC và BD trong hình bình hành ABCD. Khi đó O là trung điểm của AC, BD.
Xét ∆ABC, hai đường trung tuyến BO, CM cắt nhau tại I nên I là trọng tâm của tam giác
Suy ra \(\frac{{BI}}{{BO}} = \frac{2}{3}\) hay \(\frac{{BI}}{{\frac{1}{2}BD}} = \frac{{2BI}}{{BD}} = \frac{2}{3}\)
Do đó \(\frac{{BI}}{{BD}} = \frac{1}{3}\) (2)
Từ (1) và (2) suy ra \(\frac{{BF}}{{BE}} = \frac{1}{3}\)
Suy ra \(\frac{{D'E}}{{D'F - D'E}} = \frac{1}{{3 - 1}}\) hay \(\frac{{D'E}}{{EF}} = \frac{1}{2}\) .
Chứng minh tương tự ta cũng có \(\frac{{D'E}}{{D'F}} = \frac{{D'J}}{{D'B'}} = \frac{1}{3}\)
Suy ra \(\frac{{D'E}}{{D'F - D'E}} = \frac{1}{{3 - 1}}\) hay \(\frac{{D'E}}{{EF}} = \frac{1}{2}\)
Do đó \(\frac{{BF}}{{EF}} = \frac{{D'E}}{{EF}} = \frac{1}{2}\) nên BF = D’E = ½ EF.
Bài 9 trang 120 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 9 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 9 yêu cầu học sinh thực hiện các thao tác sau:
- Tính các biểu thức liên quan đến vectơ.
- Chứng minh đẳng thức vectơ.
- Giải các bài toán hình học sử dụng kiến thức về vectơ.
Lời giải chi tiết
Để giải bài 9 trang 120 SGK Toán 11 tập 1 - Cánh Diều, chúng ta cần nắm vững các kiến thức sau:
- Các phép toán vectơ: Cộng, trừ, nhân với một số thực.
- Tích vô hướng của hai vectơ: Định nghĩa, tính chất, ứng dụng.
- Ứng dụng của vectơ trong hình học: Chứng minh các tính chất hình học, giải các bài toán liên quan đến tam giác, hình bình hành, v.v.
Ví dụ minh họa:
Giả sử bài tập yêu cầu tính độ dài của vectơ a = (x1, y1) + (x2, y2). Ta có:
|a| = √((x1 + x2)2 + (y1 + y2)2)
Hướng dẫn giải bài tập
Để giải bài tập một cách hiệu quả, bạn nên:
- Đọc kỹ đề bài và xác định yêu cầu của bài tập.
- Vẽ hình minh họa (nếu cần thiết).
- Sử dụng các kiến thức đã học để giải bài tập.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Mở rộng kiến thức
Ngoài việc giải bài tập trong SGK, bạn nên tìm hiểu thêm các bài tập tương tự trong các nguồn tài liệu khác để nâng cao kỹ năng giải toán. Bạn cũng có thể tham khảo các video hướng dẫn giải bài tập trên internet.
Lưu ý quan trọng
Khi giải bài tập về vectơ, bạn cần chú ý đến các quy tắc về dấu và thứ tự thực hiện các phép toán. Bạn cũng nên kiểm tra lại các kết quả tính toán để tránh sai sót.
Bảng tổng hợp công thức liên quan
| Công thức | Mô tả |
|---|---|
| |a| = √(x2 + y2) | Độ dài của vectơ a = (x, y) |
| a ⋅ b = x1x2 + y1y2 | Tích vô hướng của hai vectơ a = (x1, y1) và b = (x2, y2) |
Kết luận:
Bài 9 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng. Bằng cách nắm vững các kiến thức cơ bản và rèn luyện kỹ năng giải bài tập, bạn có thể tự tin giải quyết các bài toán tương tự.
Chúc các bạn học tốt!