Bài 5 trang 120 Toán 11 tập 1 - Cánh Diều | Giải chi tiết & Chính xác

Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều

Bài 5 thuộc chương trình Toán 11 tập 1, sách Cánh Diều, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về các loại hàm số, tính đơn điệu, cực trị và ứng dụng để giải quyết các bài toán cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, BD. Điểm P thuộc cạnh AC sao cho PA = 2PC

Đề bài

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, BD. Điểm P thuộc cạnh AC sao cho PA = 2PC

a) Xác định giao điểm E của đường thẳng MP với mặt phẳng (BCD)

b) Xác định giao điểm Q của đường thẳng CD với mặt phẳng (MNP)

c) Xác định giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).

d) Gọi I là giao điểm của MQ và NP, G là trọng tâm của tam giác ABD. Chứng minh rằng C, I, G thẳng hàng.

Phương pháp giải - Xem chi tiết Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều 1

a,b, Tìm giao điểm của đường thẳng a và mặt phẳng (P) ta làm như sau: + Tìm mặt phẳng (Q) chứa a.

+ Tìm giao tuyến d của (P) và (Q).

+ Giao tuyến d cắt đường thẳng a tại I.

Suy ra, I là giao điểm của đường thẳng a và mặt phẳng (P).

c, Tìm 2 điểm cùng thuộc 2 mặt phẳng đó. Đường thẳng đi qua 2 điểm đó chính là giao tuyến của 1 mặt phẳng.

d, Chứng minh 3 điểm cùng thuộc 1 đường thẳng.

Lời giải chi tiết

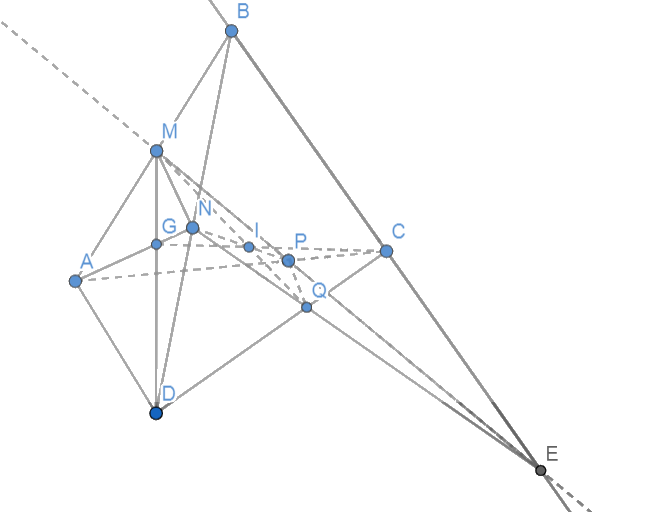
Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều 2

a) Trong mp(ABC), kéo dài MP cắt BC tại E. Nối AE, DE.

Ta có: MP ∩ BC = {E};

BC ⊂ (BCD)

Do đó MP ∩ (BCD) = {E}.

b) Nối NE, NE cắt CD tại Q.

Ta có: CD ∩ NE = {Q};

NE ⊂ (MNP)

Do đó CD ∩ (MNP) = {Q}.

c) Ta có: P ∈ AC, mà AC ⊂ (ACD) nên P ∈ (ACD);

Mà P ∈ (MNP) nên P là giao điểm của (ACD) và (MNP).

Lại có Q ∈ CD và CD ⊂ (ACD) nên Q ∈ (ACD);

Mà Q ∈ (MNP) nên Q là giao điểm của (ACD) và (MNP).

Do đó PQ là giao tuyến của hai mặt phẳng (ACD) và (MNP).

d) Do G là trọng tâm của tam giác ABD nên hai đường trung tuyến DM, AN của tam giác cùng đi qua G.

Ta có: G ∈ AN mà AN ⊂ (ANC) nên G ∈ (ANC);

G ∈ DM mà DM ⊂ (MDC) nên G ∈ (MDC).

Do đó G là giao điểm của hai mặt phẳng (ANC) và (MDC).

Lại có: C ∈ (ANC) và C ∈ (MDC) nên C cũng là giao điểm của hai mặt phẳng (ANC) và (MDC).

Vậy GC là giao tuyến của hai mặt phẳng (ANC) và (MDC).

Mặt khác, I là giao điểm của MQ và NP nên I ∈ MQ và I ∈ NP.

Vì I ∈ MQ mà MQ ⊂ (MDC) nên I ∈ (MDC)

Vì I ∈ NP mà NP ⊂ (ANC) nên I ∈ (ANC)

Do đó giao tuyến GC của hai mặt phẳng (ANC) và (MDC) đi qua điểm I.

Vậy ba điểm C, I, G thẳng hàng.

Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn

Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về hàm số và đồ thị. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này, được cung cấp bởi tusach.vn.

Nội dung bài tập

Bài 5 yêu cầu học sinh thực hiện các nhiệm vụ sau:

Xác định tập xác định của hàm số.
Tìm đạo hàm của hàm số.
Xác định các điểm cực trị của hàm số.
Vẽ đồ thị của hàm số.
Nghiên cứu sự biến thiên của hàm số.

Lời giải chi tiết

Để giải bài tập này, chúng ta cần áp dụng các kiến thức sau:

Định nghĩa hàm số và tập xác định.
Các quy tắc tính đạo hàm.
Điều kiện cần và đủ để hàm số có cực trị.
Cách vẽ đồ thị hàm số.

Ví dụ: Xét hàm số y = x³ - 3x² + 2.

Tập xác định: R
Đạo hàm: y' = 3x² - 6x
Điểm cực trị: Giải phương trình y' = 0, ta được x = 0 và x = 2. Tính y(0) = 2 và y(2) = -2. Vậy hàm số có hai điểm cực trị là (0, 2) và (2, -2).

Hướng dẫn giải bài tập tương tự

Để giải các bài tập tương tự, bạn có thể làm theo các bước sau:

Đọc kỹ đề bài và xác định yêu cầu của bài tập.
Áp dụng các kiến thức đã học để giải bài tập.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Mở rộng kiến thức

Ngoài việc giải bài tập, bạn nên tìm hiểu thêm về các ứng dụng của hàm số và đồ thị trong thực tế. Ví dụ, hàm số có thể được sử dụng để mô tả sự thay đổi của các đại lượng vật lý, kinh tế, xã hội,...

Tài liệu tham khảo

Để học tập và ôn luyện hiệu quả, bạn có thể tham khảo các tài liệu sau:

Sách giáo khoa Toán 11 tập 1 - Cánh Diều
Sách bài tập Toán 11 tập 1 - Cánh Diều
Các trang web học toán trực tuyến như tusach.vn

Lưu ý quan trọng

Khi giải bài tập về hàm số và đồ thị, bạn cần chú ý đến các yếu tố sau:

Tập xác định của hàm số.
Tính liên tục và tính khả vi của hàm số.
Các điểm cực trị của hàm số.
Bảng biến thiên của hàm số.
Đồ thị của hàm số.

tusach.vn hy vọng rằng lời giải chi tiết và hướng dẫn giải bài tập Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều sẽ giúp bạn học tập tốt hơn. Chúc bạn thành công!

Hàm số	Tập xác định	Đạo hàm
y = x²	R	y' = 2x
y = sin(x)	R	y' = cos(x)

Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều

Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều

Bài 5 trang 120 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn

Nội dung bài tập

Lời giải chi tiết

Hướng dẫn giải bài tập tương tự

Mở rộng kiến thức

Tài liệu tham khảo

Lưu ý quan trọng

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN