Bài 1 trang 116 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Bài 1 trang 116 SGK Toán 11 Tập 2 - Cánh Diều
Bài 1 thuộc chương trình học Toán 11 Tập 2, sách Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm. Bài tập này giúp học sinh củng cố kiến thức về đạo hàm của hàm số và ứng dụng vào việc giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin làm bài tập.
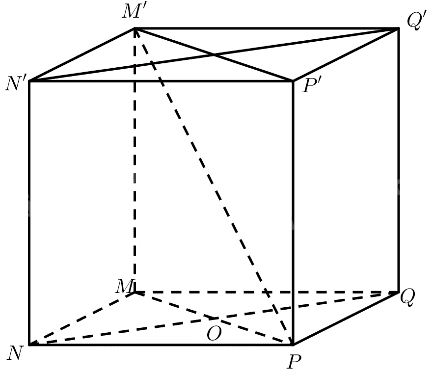
Cho hình lập phương \(MNPQ.M'N'P'Q'\) có cạnh bằng \(a\).
Đề bài
Cho hình lập phương \(MNPQ.M'N'P'Q'\) có cạnh bằng \(a\).
a) Góc giữa hai đường thẳng \(MN\) và \(M'P\) bằng:
A. \({30^ \circ }\).
B. \({45^ \circ }\).
C. \({60^ \circ }\).
D. \({90^ \circ }\).
b) Gọi \(\alpha \) là số đo góc giữa đường thẳng \(M'P\) và mặt phẳng \(\left( {MNPQ} \right)\). Giá trị \(\tan \alpha \) bằng:
A. 1.
B. 2.
C. \(\sqrt 2 \).
D. \(\frac{1}{{\sqrt 2 }}\).
c) Số đo của góc nhị diện \(\left[ {N,MM',P} \right]\) bằng:
A. \({30^ \circ }\).
B. \({45^ \circ }\).
C. \({60^ \circ }\).
D. \({90^ \circ }\).
d) Khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {NQQ'N'} \right)\) bằng:
A. \(a\).
B. \(\frac{a}{{\sqrt 2 }}\).
C. \(a\sqrt 2 \).
D. \(\frac{a}{2}\).
Phương pháp giải - Xem chi tiết
a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).
b) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
c) Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \bot c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
d) Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
a) \(MM' = PP',MM'\parallel PP'\)
\( \Rightarrow MPP'M'\) là hình bình hành
\( \Rightarrow MP\parallel M'P' \Rightarrow \left( {MN,M'P'} \right) = \left( {MN,MP} \right) = \widehat {NMP}\)
\(MNPQ\) là hình vuông \( \Rightarrow \widehat {NMP} = {45^ \circ }\)
Vậy .
Chọn B.
b) \(MM' \bot \left( {MNPQ} \right) \Rightarrow \left( {M'P,\left( {MNPQ} \right)} \right) = \left( {M'P,MP} \right) = \widehat {MPM'}\)
\(MNPQ\) là hình vuông \( \Rightarrow MP = \sqrt {M{N^2} + N{P^2}} = a\sqrt 2 \)
\(\tan \widehat {MPM'} = \frac{{MM'}}{{MP}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\)
Chọn D.
c) \(MM' \bot \left( {MNPQ} \right) \Rightarrow MM' \bot MN,MM' \bot MP\)
Vậy \(\widehat {NMP} = {45^ \circ }\) là góc nhị diện \(\left[ {N,MM',P} \right]\).
Chọn B.
d) Gọi \(O = MP \cap NQ\)
\(MNPQ\) là hình vuông \( \Rightarrow MO \bot NQ\)
\(NN' \bot \left( {MNPQ} \right) \Rightarrow NN' \bot MO\)
\( \Rightarrow d\left( {M,\left( {NQQ'N'} \right)} \right) = MO = \frac{1}{2}MP = \frac{a}{{\sqrt 2 }}\).
Chọn B.
Bài 1 trang 116 SGK Toán 11 Tập 2 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 1 trang 116 SGK Toán 11 Tập 2 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này, được cung cấp bởi tusach.vn.
Nội dung bài tập
Bài 1 yêu cầu học sinh tính đạo hàm của các hàm số sau:
- a) y = x3 - 3x2 + 2x - 5
- b) y = (x2 + 1)(x - 2)
- c) y = (x2 + 3x + 1) / (x + 1)
- d) y = sin(2x + 1)
Lời giải chi tiết
Để giải bài tập này, chúng ta cần sử dụng các quy tắc tính đạo hàm cơ bản, bao gồm:
- Đạo hàm của một tổng: (u + v)' = u' + v'
- Đạo hàm của một tích: (uv)' = u'v + uv'
- Đạo hàm của một thương: (u/v)' = (u'v - uv') / v2
- Đạo hàm của một hàm hợp: (f(g(x)))' = f'(g(x)) * g'(x)
- Đạo hàm của các hàm số cơ bản: (xn)' = nxn-1, (sin x)' = cos x, ...
Giải chi tiết từng câu
a) y = x3 - 3x2 + 2x - 5
y' = 3x2 - 6x + 2
b) y = (x2 + 1)(x - 2)
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
c) y = (x2 + 3x + 1) / (x + 1)
y' = ((2x + 3)(x + 1) - (x2 + 3x + 1)(1)) / (x + 1)2 = (2x2 + 5x + 3 - x2 - 3x - 1) / (x + 1)2 = (x2 + 2x + 2) / (x + 1)2
d) y = sin(2x + 1)
y' = cos(2x + 1) * 2 = 2cos(2x + 1)
Lưu ý khi giải bài tập
Khi giải bài tập về đạo hàm, cần chú ý:
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Áp dụng đúng quy tắc cho từng hàm số.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tại sao nên chọn tusach.vn để học Toán 11?
tusach.vn là một nguồn tài liệu học tập Toán 11 uy tín và chất lượng, cung cấp:
- Lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK.
- Bài giảng video hấp dẫn, giúp học sinh nắm vững kiến thức.
- Các bài tập trắc nghiệm và bài tập tự luyện để rèn luyện kỹ năng.
- Đội ngũ giáo viên giàu kinh nghiệm, sẵn sàng hỗ trợ học sinh.
Hãy truy cập tusach.vn ngay hôm nay để học Toán 11 hiệu quả và đạt kết quả cao!