Lý thuyết Hai mặt phẳng vuông góc - Toán 11 Cánh diều
Tổng quan nội dung
Lý thuyết Hai mặt phẳng vuông góc - Toán 11 Cánh diều
Bài học này cung cấp kiến thức nền tảng về hai mặt phẳng vuông góc trong chương trình Hình học không gian lớp 11, sách Cánh diều.
Chúng ta sẽ cùng tìm hiểu định nghĩa, điều kiện nhận biết hai mặt phẳng vuông góc, và các tính chất quan trọng liên quan.
Nắm vững lý thuyết này là bước đệm quan trọng để giải quyết các bài toán thực tế và nâng cao kết quả học tập môn Toán.
1. Định nghĩa Hai mặt phẳng cắt nhau tạo nên bốn góc nhị diện. Nếu một trong các góc nhị diện đó là hai góc nhị diện vuông thì hai mặt phẳng đã cho gọi là vuông góc với nhau.
1. Định nghĩa
Hai mặt phẳng cắt nhau tạo nên bốn góc nhị diện. Nếu một trong các góc nhị diện đó là hai góc nhị diện vuông thì hai mặt phẳng đã cho gọi là vuông góc với nhau.
Ví dụ: Hai mặt phẳng (P) và (Q) cắt nhau tạo nên bốn góc nhị diện. Nếu một trong bốn góc nhị diện đó là góc nhị diện vuông thì vta nói (P) vuông góc với (Q), kí hiệu là \(\left( P \right) \bot \left( Q \right)\) hoặc \(\left( Q \right) \bot \left( P \right)\).
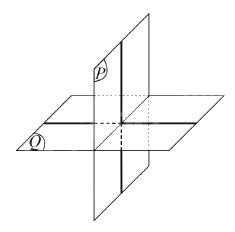
2. Điều kiện để hai mặt phẳng vuông góc
Nếu mặt phẳng này chứa một đường thẳng mà đường thẳng đó vuông góc với mặt phẳng kia thì hai mặt phẳng đó vuông góc với nhau.
3. Tính chất
- Tính chất 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cùng vuông góc với mặt phẳng kia.
- Tính chất 2: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
Nhận xét:
- Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Nếu qua một điểm trong mặt phẳng (P) ta dựng đường thẳng vuông góc với mặt phẳng (Q) thì đường thẳng này nằm trong mặt phẳng (P).
- Nếu hai mặt phẳng vuông góc với nhau thì hình chiếu của một đường thẳng nằm trong mặt phẳng này trên mặt phẳng kia đều trùng hoặc nằm trên giao tuyến.
- Ta có thể chứng minh đường thẳng vuông góc với mặt phẳng bằng cách sử dụng Tính chất 1.
Lý Thuyết Hai Mặt Phẳng Vuông Góc - Toán 11 Cánh Diều: Giải Thích Chi Tiết & Bài Tập
Chào mừng các em học sinh lớp 11 đến với bài học về Lý thuyết Hai mặt phẳng vuông góc, thuộc chương trình Hình học không gian của sách Toán 11 Cánh diều. Đây là một trong những kiến thức quan trọng, nền tảng để các em có thể giải quyết các bài toán phức tạp hơn trong tương lai. Bài viết này sẽ cung cấp cho các em một cách đầy đủ, dễ hiểu về lý thuyết này, kèm theo các ví dụ minh họa và bài tập vận dụng để các em có thể nắm vững kiến thức.
1. Định Nghĩa Hai Mặt Phẳng Vuông Góc
Hai mặt phẳng được gọi là vuông góc với nhau khi và chỉ khi góc giữa hai mặt phẳng đó bằng 90°. Để xác định góc giữa hai mặt phẳng, ta thường sử dụng đường thẳng vuông góc với cả hai mặt phẳng. Đường thẳng này tạo với mỗi mặt phẳng một góc, và góc nhỏ hơn hoặc bằng 90° trong hai góc tạo thành là góc giữa hai mặt phẳng.
2. Điều Kiện Nhận Biết Hai Mặt Phẳng Vuông Góc
Có một số điều kiện để nhận biết hai mặt phẳng vuông góc:
- Điều kiện 1: Một đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.
- Điều kiện 2: Mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
- Điều kiện 3: Góc giữa hai mặt phẳng bằng 90°.
Các em cần nắm vững các điều kiện này để có thể xác định hai mặt phẳng có vuông góc hay không trong các bài toán cụ thể.
3. Tính Chất của Hai Mặt Phẳng Vuông Góc
Khi hai mặt phẳng vuông góc, một số tính chất quan trọng sau đây được thỏa mãn:
- Nếu một đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng, thì nó vuông góc với mặt phẳng kia.
- Nếu một mặt phẳng chứa một đường thẳng vuông góc với mặt phẳng kia, thì hai mặt phẳng đó vuông góc với nhau.
4. Ví Dụ Minh Họa
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Biết SA vuông góc với mặt phẳng (ABCD). Chứng minh rằng (SAD) vuông góc với (SBC).
Giải:
- Vì SA vuông góc với (ABCD) nên SA vuông góc với AD. Do đó, (SAD) vuông góc với AD.
- Vì ABCD là hình vuông nên BC vuông góc với AD.
- Từ (1) và (2) suy ra AD vuông góc với (SBC).
- Vậy (SAD) vuông góc với (SBC).
5. Bài Tập Vận Dụng
Bài tập 1: Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau. Chứng minh rằng:
- (SAB) vuông góc với (SAC).
- (SBC) vuông góc với (SCA).
- (SCA) vuông góc với (SAB).
Bài tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chứng minh rằng (ABCD) vuông góc với (ADD'A').
6. Lời Khuyên Khi Học Lý Thuyết Hai Mặt Phẳng Vuông Góc
- Nắm vững định nghĩa: Hiểu rõ khái niệm về góc giữa hai mặt phẳng và điều kiện để hai mặt phẳng vuông góc.
- Vẽ hình: Luôn vẽ hình minh họa khi giải bài tập để dễ dàng hình dung và tìm ra hướng giải quyết.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và củng cố kiến thức.
- Sử dụng tài liệu tham khảo: Tham khảo thêm các tài liệu, sách giáo khoa, và trang web uy tín để có thêm thông tin và kiến thức.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về Lý thuyết Hai mặt phẳng vuông góc - Toán 11 Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!