Giải mục 1 trang 110, 111 SGK Toán 11 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 110, 111 sách giáo khoa Toán 11 tập 1 chương trình Cánh Diều. Bài viết này sẽ giúp các em hiểu rõ hơn về nội dung bài học và tự tin giải các bài tập liên quan.
tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp những tài liệu học tập chất lượng và dễ hiểu nhất.
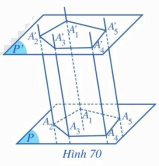
Cho hai mặt phẳng song song (P) và (P’). Trong mặt phẳng (P), cho đa giác \({A_1}{A_2}...{A_n}\) .Qua các đỉnh \({A_1},{A_2},...,{A_n}\) vẽ các đường thẳng song song với nhau và cắt mặt phẳng (P) lần lượt tại\(A_1^',A_2^',...,A_n^'\) (Hình 70 minh họa cho trường hợp n = 5).
Giải mục 1 trang 110, 111 SGK Toán 11 tập 1 - Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Mục 1 trang 110, 111 SGK Toán 11 tập 1 chương trình Cánh Diều tập trung vào việc ôn tập chương 1: Hàm số lượng giác và đồ thị. Đây là một phần quan trọng trong chương trình Toán 11, đặt nền móng cho các kiến thức tiếp theo. Việc nắm vững các khái niệm và kỹ năng trong mục này sẽ giúp các em giải quyết các bài toán phức tạp hơn một cách dễ dàng.
Nội dung chính của Mục 1
- Ôn tập lý thuyết: Các kiến thức cơ bản về hàm số lượng giác (sin, cos, tan, cot), tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ, và đồ thị của các hàm số này.
- Các dạng bài tập thường gặp:
- Xác định tập xác định của hàm số lượng giác.
- Tìm tập giá trị của hàm số lượng giác.
- Kiểm tra tính chẵn lẻ của hàm số lượng giác.
- Vẽ đồ thị hàm số lượng giác.
- Giải phương trình lượng giác cơ bản.
Hướng dẫn giải chi tiết các bài tập trong Mục 1
Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 1 trang 110, 111 SGK Toán 11 tập 1 - Cánh Diều:
Bài 1: (Trang 110)
Bài 1 yêu cầu xác định tập xác định của các hàm số lượng giác. Để giải bài này, các em cần nhớ lại điều kiện xác định của từng hàm số lượng giác. Ví dụ, hàm số y = tan(x) xác định khi cos(x) ≠ 0.
Bài 2: (Trang 110)
Bài 2 yêu cầu tìm tập giá trị của các hàm số lượng giác. Để giải bài này, các em cần nhớ lại khoảng giá trị của từng hàm số lượng giác. Ví dụ, -1 ≤ sin(x) ≤ 1.
Bài 3: (Trang 111)
Bài 3 yêu cầu kiểm tra tính chẵn lẻ của các hàm số lượng giác. Để giải bài này, các em cần nhớ lại định nghĩa về hàm số chẵn và hàm số lẻ. Một hàm số f(x) là hàm số chẵn nếu f(-x) = f(x) với mọi x thuộc tập xác định. Một hàm số f(x) là hàm số lẻ nếu f(-x) = -f(x) với mọi x thuộc tập xác định.
Mẹo học tập hiệu quả
- Nắm vững lý thuyết: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các khái niệm và công thức quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Sử dụng tài liệu tham khảo: Tham khảo các sách bài tập, đề thi thử, và các trang web học tập trực tuyến để mở rộng kiến thức.
- Hỏi thầy cô giáo: Nếu gặp khó khăn trong quá trình học tập, đừng ngần ngại hỏi thầy cô giáo để được giải đáp.
Bảng tổng hợp công thức lượng giác quan trọng
| Công thức | Mô tả |
|---|
| sin2(x) + cos2(x) = 1 | Công thức lượng giác cơ bản |
| tan(x) = sin(x) / cos(x) | Công thức tính tan(x) |
| cot(x) = cos(x) / sin(x) | Công thức tính cot(x) |
Hy vọng với những hướng dẫn chi tiết và mẹo học tập trên, các em sẽ tự tin giải quyết các bài tập trong Mục 1 trang 110, 111 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tốt!