Giải mục 2 và 3 trang 9, 10, 11, 12, 13, 14, 15 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Giải Bài Tập Mục 2 & 3 SGK Toán 11 Tập 1 Cánh Diều
Chào mừng bạn đến với trang giải bài tập Toán 11 tập 1 Cánh Diều của tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Trang này cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong mục 2 và 3 trang 9 đến 15, giúp bạn hiểu rõ bản chất của bài học và tự tin giải quyết các bài tập tương tự.
Hoạt động 6: a) Trong mặt phẳng tọa độ ( định hướng) Oxy, hãy vẽ đường tròn tâm O với bán kính bằng 1.
HĐ6
a) Trong mặt phẳng tọa độ (định hướng) Oxy, hãy vẽ đường tròn tâm O và bán kính bằng 1
b) Hãy nêu chiều dương, chiều âm trên đường tròn tâm O với bán kính bằng 1
Phương pháp giải:
Dựa vào kiến thực đã học về trục tọa độ và kiến thức học ở phần trên để xác vẽ hình
Lời giải chi tiết:
a) b)
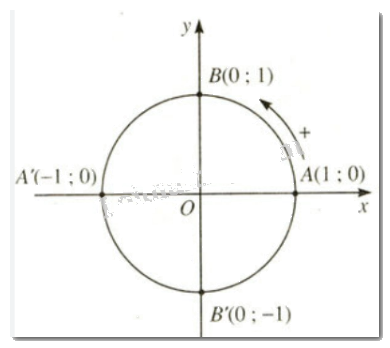
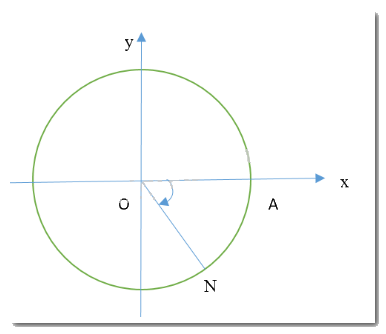
LT-VD6
Xác định điểm N trên đường tròn lượng giác sao cho \(\left( {OA,ON} \right) = - \frac{\pi }{3}\)
Phương pháp giải:
Dựa vào kiến thực đã học về trục tọa độ và kiến thức học ở phần trên để xác vẽ
Lời giải chi tiết:

HĐ7
a) Xác định điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = 60^\circ \)
b) So sánh hoành độ của điểm M với \(\cos 60^\circ \); tung độ của điểm M với \(\sin 60^\circ \)
Phương pháp giải:
Dựa vào cách xác định góc bên trên để xác định
Lời giải chi tiết:
a) 
b) \(\cos 60^\circ \) bằng hoành độ của điểm M
\(\sin 60^\circ \) bằng tung độ của điểm M
LT-VD7
Tìm giác trị lượng giác của góc lượng giác \(\beta = - \frac{\pi }{4}\)
Phương pháp giải:
Dựa vào kiến thức đã học để tính
Lời giải chi tiết:
\(\sin \left( { - \frac{\pi }{4}} \right) = - \frac{{\sqrt 2 }}{2};\,\,\cos \left( { - \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( { - \frac{\pi }{4}} \right) = - \frac{1}{2};\,\,\cot \left( { - \frac{\pi }{4}} \right) = - 2\)
HĐ8
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = - 30^\circ \)
Phương pháp giải:
Dựa vào sin, cos, tan, cot đã học ở lớp dưới để xác định
Lời giải chi tiết:
\(\begin{array}{l}\cos \left( { - 30^\circ } \right) = \frac{{\sqrt 3 }}{2} > 0\\\sin \left( { - 30^\circ } \right) = - \frac{1}{2} < 0\\\tan \left( { - 30^\circ } \right) = - \frac{{\sqrt 3 }}{3} < 0\\\cot \left( { - 30^\circ } \right) = - \sqrt 3 < 0\end{array}\)
LT-VD8
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\)
Phương pháp giải:
Dựa vào bảng xét dấu sau:

Lời giải chi tiết:
Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi \) nên
\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{6}} \right) < 0\\\sin \left( {\frac{{5\pi }}{6}} \right) > 0\\\tan \left( {\frac{{5\pi }}{6}} \right) < 0\\\cot \left( {\frac{{5\pi }}{6}} \right) < 0\end{array}\)
HĐ9
Cho góc lượng giác \(\alpha \). So sánh
a) \({\cos ^2}\alpha + {\sin ^2}\alpha \,\,\) và 1
b) \(\tan \alpha .\cot \alpha \,\,\) và 1 với \(\cos \alpha \ne 0;\sin \alpha \ne 0\)
c) \(1 + {\tan ^2}\alpha \,\,\) và \(\frac{1}{{{{\cos }^2}\alpha }}\) với \(\cos \alpha \ne 0\)
d) \(1 + {\cot ^2}\alpha \,\) và \(\frac{1}{{{{\sin }^2}\alpha }}\) với \(\sin \alpha \ne 0\)
Phương pháp giải:
Dựa vào kiến thức của phần phía trên và kiến thức lớp 9 để so sánh
Lời giải chi tiết:
a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
b) \(\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\)
c) \(\frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha + 1\)
d) \(\frac{1}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = 1 + {\cot ^2}\alpha \)
LT-VD9
Cho góc lượng giác \(\alpha \)sao cho \(\pi < \alpha < \frac{{3\pi }}{2}\) và \(\sin \alpha = - \frac{4}{5}\). Tìm \(\cos \alpha \)
Phương pháp giải:
Sử dụng công thức lượng giác \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
Lời giải chi tiết:
Vì \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\) nên \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( { - \frac{4}{5}} \right)^2} = \frac{9}{{25}}\)
Do \(\pi < \alpha < \frac{{3\pi }}{2}\) nên \(\cos \alpha < 0\). Suy ra \(\cos \alpha = - \frac{3}{5}\)
HĐ10
Tìm các giá trị lượng giác của góc lượng giác \(\alpha = 45^\circ \)
Phương pháp giải:
Dựa vào các kiến thức đã học để tính
Lời giải chi tiết:
\(\sin \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\cos \left( {45^\circ } \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( {45^\circ } \right) = \frac{1}{2};\,\,\cot \left( {45^\circ } \right) = 2\)
LT-VD10
Tính giá trị của biểu thức:
\(Q = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + \cos \frac{\pi }{2}\)
Phương pháp giải:
Sử dựng bảng lượng giác của các góc đặc biệt

Lời giải chi tiết:
Ta có
\(\begin{array}{l}Q = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + \cos \frac{\pi }{2}\\\,\,\,\,\, = \,{\left( {\sqrt 3 } \right)^2} + {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} + 1 + 0 = \frac{7}{2}\end{array}\)
HĐ11
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác \(\left( {OA,OM} \right) = \alpha ,\,\,\left( {OA,OM'} \right) = - \alpha \) (Hình 13)

a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.
b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \) và \(- \alpha \)
Phương pháp giải:
Dựa vào hình vẽ ( hình 13)
Lời giải chi tiết:
a) Hoành độ của điểm M và M’ bằng nhau
Tung độ của điểm M và M’ đối nhau
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha\) và \(- \alpha \)
LT-VD11
a) \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8}\)
b) \(\tan {1^ \circ }.\tan {2^ \circ }.\tan {45^ \circ }.\tan {88^ \circ }.\tan {89^ \circ }\)
Phương pháp giải:
Sử dụng công thức trong bảng:

Lời giải chi tiết:
a) \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8} = {\cos ^2}\frac{\pi }{8} + {\cos ^2}\left( {\frac{\pi }{2} - \frac{\pi }{8}} \right) = {\cos ^2}\frac{\pi }{8} + {\sin ^2}\frac{\pi }{8} = 1\)
b)
\(\begin{array}{l}\tan {1^ \circ }.\tan {2^ \circ }.\tan {45^ \circ }.\tan {88^ \circ }.\tan {89^ \circ }\\ = (\tan {1^ \circ }.\tan {89^ \circ }).(\tan {2^ \circ }.\tan {88^ \circ }).\tan {45^ \circ }\\ = (\tan {1^ \circ }.\cot {1^ \circ }).(\tan {2^ \circ }.\cot {2^ \circ }).\tan {45^ \circ }\\ = 1\end{array}\)
LT-VD12
Dùng máy tính cầm tay để tính ;
a) \(\tan ( - {75^ \circ });\)b) \(\cot \left( { - \frac{\pi }{5}} \right)\)
Phương pháp giải:
Sử dụng máy tính cầm tay
Lời giải chi tiết:
a) \(\tan ( - {75^ \circ }) = - 2 - \sqrt 3 \)
b) \(\cot \left( { - \frac{\pi }{5}} \right) \approx - 1,376\)
Giải Chi Tiết Mục 2 & 3 SGK Toán 11 Tập 1 Cánh Diều - tusach.vn
Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 Cánh Diều, đặc biệt là phần mục 2 và 3 trang 9 đến 15. Tusach.vn tự hào là người bạn đồng hành đáng tin cậy trong quá trình học tập của các em.
Tổng Quan Về Mục 2 & 3 Toán 11 Tập 1 Cánh Diều
Mục 2 và 3 trong SGK Toán 11 tập 1 Cánh Diều tập trung vào các kiến thức cơ bản về hàm số bậc hai và bất phương trình bậc hai. Đây là nền tảng quan trọng cho các kiến thức nâng cao hơn trong chương trình học. Các em sẽ được làm quen với:
- Định nghĩa hàm số bậc hai.
- Các dạng biểu diễn của hàm số bậc hai (dạng tổng quát, dạng chuẩn).
- Đồ thị của hàm số bậc hai (parabol).
- Các yếu tố của parabol (đỉnh, trục đối xứng, tiêu điểm, đường chuẩn).
- Giải bất phương trình bậc hai.
- Ứng dụng của hàm số bậc hai và bất phương trình bậc hai trong thực tế.
Hướng Dẫn Giải Bài Tập Chi Tiết
Dưới đây là phần giải chi tiết các bài tập trong mục 2 và 3, trang 9 đến 15 SGK Toán 11 tập 1 Cánh Diều. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng để các em có thể tự học hiệu quả.
Bài 1: (Trang 9)
(Nội dung bài tập và lời giải chi tiết)
Bài 2: (Trang 10)
(Nội dung bài tập và lời giải chi tiết)
Bài 3: (Trang 11)
(Nội dung bài tập và lời giải chi tiết)
Bài 4: (Trang 12)
(Nội dung bài tập và lời giải chi tiết)
Bài 5: (Trang 13)
(Nội dung bài tập và lời giải chi tiết)
Bài 6: (Trang 14)
(Nội dung bài tập và lời giải chi tiết)
Bài 7: (Trang 15)
(Nội dung bài tập và lời giải chi tiết)
Mẹo Giải Bài Tập Toán 11 Hiệu Quả
Để giải bài tập Toán 11 hiệu quả, các em nên:
- Nắm vững kiến thức cơ bản về hàm số và bất phương trình bậc hai.
- Luyện tập thường xuyên các bài tập từ dễ đến khó.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ đồ thị.
- Tham khảo các nguồn tài liệu học tập khác nhau (sách giáo khoa, sách bài tập, internet).
- Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.
Tại Sao Nên Chọn tusach.vn?
Tusach.vn cam kết cung cấp:
- Lời giải chính xác, chi tiết, dễ hiểu.
- Đội ngũ giáo viên giàu kinh nghiệm.
- Cập nhật liên tục các bài giải mới nhất.
- Giao diện thân thiện, dễ sử dụng.
- Hỗ trợ 24/7.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Chúc các em học tập tốt!