Bài 2 trang 113 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Bài 2 trang 113 SGK Toán 11 Tập 1 - Cánh Diều
Bài 2 thuộc chương trình học Toán 11 Tập 1, sách Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm giới hạn của hàm số tại một điểm cho trước.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin làm bài tập.
Cho hình hộp ABCD.A’B’C’D‘. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA‘, C’D‘, AD‘. Chứng minh rằng:
Đề bài
Cho hình hộp ABCD.A’B’C’D‘. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA‘, C’D‘, AD‘. Chứng minh rằng:
a) NQ // A’D‘ và \(NQ = \frac{1}{2}A'D'\)
b) Tứ giác MNQC là hình bình hành
c) MN // (ACD‘)
d) (MNP) // (ACD‘)
Phương pháp giải - Xem chi tiết
- Hình tứ giác có các cặp cạnh song song là hình bình hành
- Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với (P)
- Nếu mặt phẳng (P) chứa hai đường thằng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)
Lời giải chi tiết
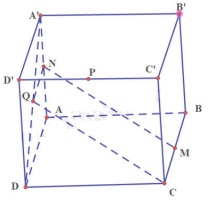
a) Ta có: N là trung điểm của AA’ nên \(\frac{{AN}}{{AA'}} = \frac{1}{2}\)
Q là trung điểm của AD’ nên \(\frac{{AQ}}{{AD'}} = \frac{1}{2}\)
Theo định lý Ta – let, ta có NQ // A’D’
Suy ra \(\frac{{NQ}}{{A'D'}} = \frac{{AN}}{{AA'}} = \frac{1}{2}\) nên\(NQ = \frac{1}{2}A'D'\)
b) Ta có: NQ // A’D’ mà A’D’ // BC nên NQ // BC hay NQ // MC (1)
Ta có \(NQ = \frac{1}{2}A'D'\) mà A’D’ = BC, \(MC = \frac{1}{2}BC\), nên NQ = MC (2)
Từ (1) và (2) suy ra MNQC là hình bình hành
c) Ta có: MNQC là hình bình hành nên MN // CQ
Mà CQ thuộc (ACD’)
Nên MN // (ACD’)
d) Gọi O là trung điểm của AC
Tam giác ACB có: O, M là trung điểm của AC, BC
Suy ra: OM // AB nên \(OM = \frac{1}{2}AB\)
Mà AB = C’D’, \(D'P = \frac{1}{2}C'D\),
Suy ra OM = D’P (1)
Ta có: OM // AB, AB // C’D’ nên OM // C’D‘ hay OM // D’P (2)
Từ (1) và (2) suy ra OMPD’ là hình bình hành. Do đó: MP // OD’
Mà OD’ thuộc (ACD’)
Suy ra: MP // (ACD’)
Mà MN thuộc (ACD’)
Do đó: (MNP) // (ACD’)
Giải chi tiết Bài 2 trang 113 SGK Toán 11 Tập 1 - Cánh Diều
Bài 2 trang 113 SGK Toán 11 Tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn hàm số. Dưới đây là lời giải chi tiết cho từng phần của bài tập:
Phần a: Tính giới hạn limx→2 (x2 - 3x + 2) / (x - 2)
Để tính giới hạn này, ta có thể phân tích tử thức thành nhân tử:
x2 - 3x + 2 = (x - 1)(x - 2)
Vậy, limx→2 (x2 - 3x + 2) / (x - 2) = limx→2 (x - 1)(x - 2) / (x - 2) = limx→2 (x - 1) = 2 - 1 = 1
Phần b: Tính giới hạn limx→-1 (x3 + 1) / (x + 1)
Tương tự, ta phân tích tử thức:
x3 + 1 = (x + 1)(x2 - x + 1)
Vậy, limx→-1 (x3 + 1) / (x + 1) = limx→-1 (x + 1)(x2 - x + 1) / (x + 1) = limx→-1 (x2 - x + 1) = (-1)2 - (-1) + 1 = 1 + 1 + 1 = 3
Phần c: Tính giới hạn limx→0 sin(x) / x
Đây là một giới hạn lượng giác cơ bản. Ta biết rằng limx→0 sin(x) / x = 1
Phần d: Tính giới hạn limx→1 (√(x+3) - 2) / (x - 1)
Để tính giới hạn này, ta sử dụng phương pháp nhân liên hợp:
limx→1 (√(x+3) - 2) / (x - 1) = limx→1 [(√(x+3) - 2)(√(x+3) + 2)] / [(x - 1)(√(x+3) + 2)] = limx→1 (x + 3 - 4) / [(x - 1)(√(x+3) + 2)] = limx→1 (x - 1) / [(x - 1)(√(x+3) + 2)] = limx→1 1 / (√(x+3) + 2) = 1 / (√(1+3) + 2) = 1 / (2 + 2) = 1/4
Lưu ý khi giải bài tập về giới hạn
- Phân tích tử thức và mẫu thức: Tìm cách phân tích thành nhân tử hoặc sử dụng các công thức lượng giác để đơn giản biểu thức.
- Sử dụng phương pháp nhân liên hợp: Đặc biệt hữu ích khi có căn thức trong biểu thức.
- Áp dụng các giới hạn lượng giác cơ bản: limx→0 sin(x) / x = 1, limx→0 (1 - cos(x)) / x = 0.
- Kiểm tra điều kiện xác định: Đảm bảo rằng biểu thức có nghĩa tại điểm giới hạn.
Tại sao nên chọn tusach.vn để học Toán 11?
tusach.vn là một nguồn tài liệu học tập Toán 11 uy tín và chất lượng. Chúng tôi cung cấp:
- Lời giải chi tiết, dễ hiểu: Được trình bày rõ ràng, logic, giúp học sinh nắm vững kiến thức.
- Đáp án chính xác: Được kiểm tra kỹ lưỡng bởi đội ngũ giáo viên chuyên môn.
- Nội dung cập nhật liên tục: Theo sát chương trình học mới nhất.
- Giao diện thân thiện, dễ sử dụng: Tạo trải nghiệm học tập tốt nhất cho học sinh.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập Toán 11 hữu ích!