Giải mục 1 trang 77 SGK Toán 11 tập 2 - Cánh Diều
Tổng quan nội dung
Giải mục 1 trang 77 SGK Toán 11 tập 2 - Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài tập mục 1 trang 77 SGK Toán 11 tập 2, sách Cánh Diều. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp lời giải dễ hiểu, kèm theo các bước giải chi tiết và ví dụ minh họa.
Trong mặt phẳng cho hai đường thẳng a, b.
Hoạt động 1
Trong mặt phẳng cho hai đường thẳng a, b.
a) Nếu a và b cắt nhau tại O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào?
b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?
c) Nếu a và b trùng nhau thì góc giữa a và b bằng bao nhiêu độ?
Phương pháp giải:
Dựa vào các kiến thức đã học trong mặt phẳng để trả lời câu hỏi
Lời giải chi tiết:
a) Nếu a và b cắt nhau tại O thì: \(0^\circ \le \left( {a,b} \right) \le 90^\circ \)
b) Nếu a // b thì không có góc tạo bởi a và b
c) Nếu a và b trùng nhau thì góc giữa a và b bằng \(0^\circ \)
Luyện tập – Vận dụng 1
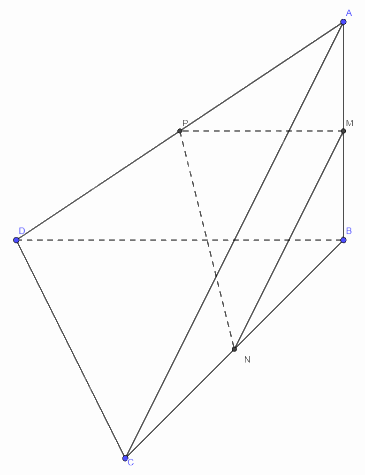
Cho tứ diện ABCD có M, N, P lần lượt là trung điểm của AB, BC, DA. Biết tam giác MNP đều. Tính góc giữa hai đường thẳng AC và BD.

Phương pháp giải:
Dựa vào kiến thức vừa học để làm bài
Lời giải chi tiết:
Xét \(\Delta ACB\)có:
N là trung điểm BC
M là trung điểm AB
=> MN là đường trung bình của tam giác ABC
=> MN // AC
Xét tam giác ABD có:
P là trung điểm AD
M là trung điểm AB
=> MP là đường trung bình của tam giác ABD
=> MP // BD
Ta có \(\left( {AC;BD} \right) = \left( {MN;MP} \right) = \widehat {NMP} = 60^\circ \)
Giải mục 1 trang 77 SGK Toán 11 tập 2 - Cánh Diều: Tổng quan và Phương pháp giải
Mục 1 trang 77 SGK Toán 11 tập 2 Cánh Diều thường xoay quanh các bài toán về đạo hàm của hàm số. Đây là một phần kiến thức quan trọng trong chương trình Toán 11, làm nền tảng cho các kiến thức nâng cao hơn ở các lớp trên. Việc nắm vững phương pháp giải các bài toán này không chỉ giúp học sinh đạt điểm cao trong các bài kiểm tra mà còn rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Nội dung chính của Mục 1 trang 77
- Ôn tập về đạo hàm: Nhắc lại các công thức đạo hàm cơ bản của các hàm số thường gặp như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
- Đạo hàm của hàm hợp: Giải các bài toán tính đạo hàm của hàm hợp, sử dụng quy tắc đạo hàm của hàm hợp.
- Đạo hàm của hàm ẩn: Giải các bài toán tìm đạo hàm của hàm ẩn, sử dụng phương pháp lấy đạo hàm hai vế.
- Ứng dụng của đạo hàm: Giải các bài toán liên quan đến việc tìm cực trị của hàm số, khảo sát hàm số.
Hướng dẫn giải chi tiết các bài tập trong Mục 1 trang 77
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong Mục 1 trang 77 SGK Toán 11 tập 2 Cánh Diều:
Bài 1: Tính đạo hàm của các hàm số sau
Để giải bài tập này, học sinh cần nắm vững các công thức đạo hàm cơ bản và quy tắc đạo hàm. Ví dụ, để tính đạo hàm của hàm số y = x2 + 3x - 2, ta sử dụng công thức đạo hàm của hàm đa thức:
y' = 2x + 3
Bài 2: Tính đạo hàm của hàm hợp
Để giải bài tập này, học sinh cần sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x). Ví dụ, để tính đạo hàm của hàm số y = sin(x2), ta có:
y' = cos(x2) * 2x = 2x * cos(x2)
Bài 3: Tìm đạo hàm của hàm ẩn
Để giải bài tập này, học sinh cần lấy đạo hàm hai vế của phương trình và sử dụng quy tắc đạo hàm của hàm ẩn. Ví dụ, nếu x2 + y2 = 1, ta có:
2x + 2y * y' = 0 => y' = -x/y
Mẹo giải nhanh và hiệu quả
- Nắm vững các công thức đạo hàm cơ bản: Đây là nền tảng để giải quyết mọi bài toán về đạo hàm.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải.
- Sử dụng các công cụ hỗ trợ: Các công cụ tính đạo hàm online có thể giúp kiểm tra lại kết quả và tiết kiệm thời gian.
- Hiểu rõ bản chất của vấn đề: Đừng chỉ học thuộc công thức mà hãy cố gắng hiểu rõ ý nghĩa của từng bước giải.
Tài liệu tham khảo thêm
Ngoài SGK Toán 11 tập 2 Cánh Diều, học sinh có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11
- Các trang web học Toán online
- Các video hướng dẫn giải Toán 11 trên YouTube
Kết luận
Giải mục 1 trang 77 SGK Toán 11 tập 2 Cánh Diều đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và luyện tập thường xuyên. Hy vọng với hướng dẫn chi tiết và các mẹo giải nhanh trên, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.